Bridging the Gap between Community and Node Representations: Graph Embedding via Community Detection

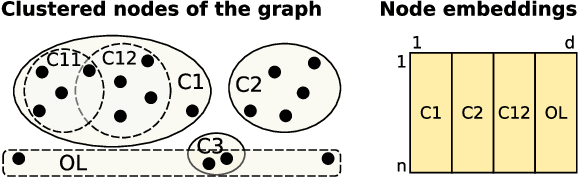
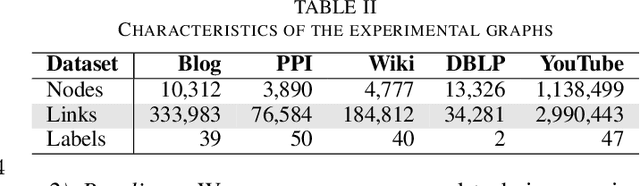
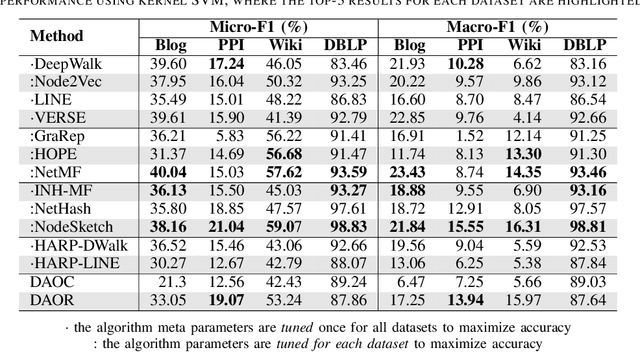
Graph embedding has become a key component of many data mining and analysis systems. Current graph embedding approaches either sample a large number of node pairs from a graph to learn node embeddings via stochastic optimization or factorize a high-order proximity/adjacency matrix of the graph via computationally expensive matrix factorization techniques. These approaches typically require significant resources for the learning process and rely on multiple parameters, which limits their applicability in practice. Moreover, most of the existing graph embedding techniques operate effectively in one specific metric space only (e.g., the one produced with cosine similarity), do not preserve higher-order structural features of the input graph and cannot automatically determine a meaningful number of embedding dimensions. Typically, the produced embeddings are not easily interpretable, which complicates further analyses and limits their applicability. To address these issues, we propose DAOR, a highly efficient and parameter-free graph embedding technique producing metric space-robust, compact and interpretable embeddings without any manual tuning. Compared to a dozen state-of-the-art graph embedding algorithms, DAOR yields competitive results on both node classification (which benefits form high-order proximity) and link prediction (which relies on low-order proximity mostly). Unlike existing techniques, however, DAOR does not require any parameter tuning and improves the embeddings generation speed by several orders of magnitude. Our approach has hence the ambition to greatly simplify and speed up data analysis tasks involving graph representation learning.

DAOC: Stable Clustering of Large Networks

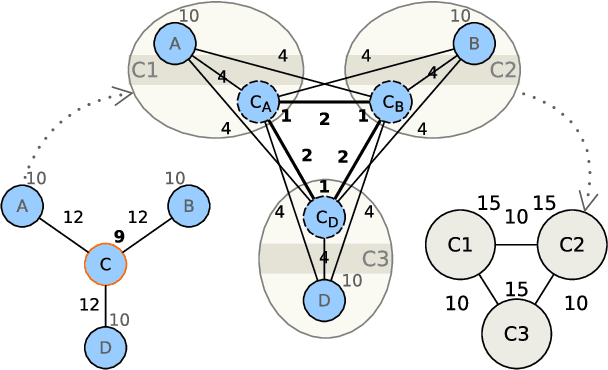
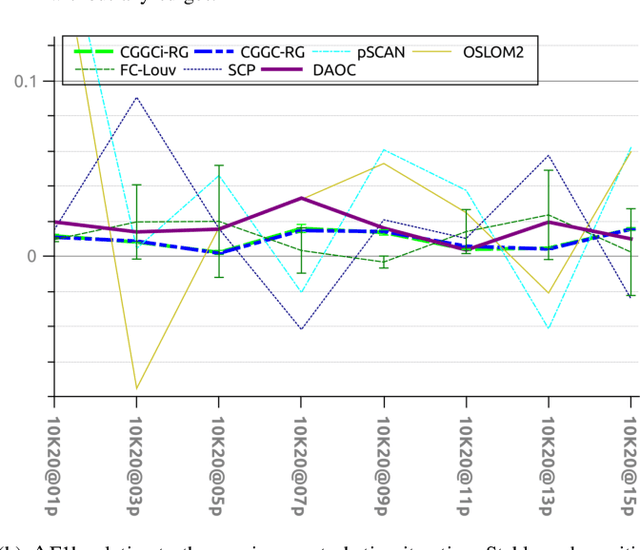
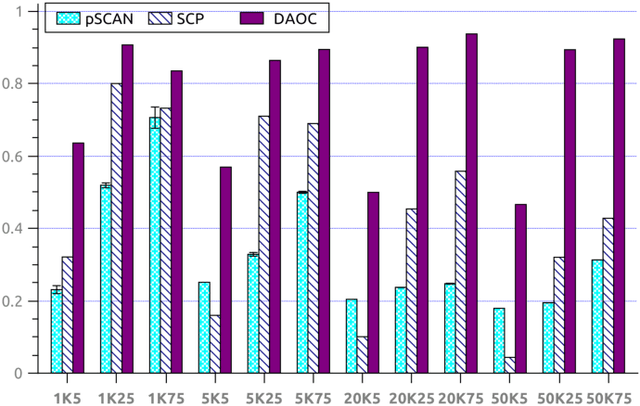
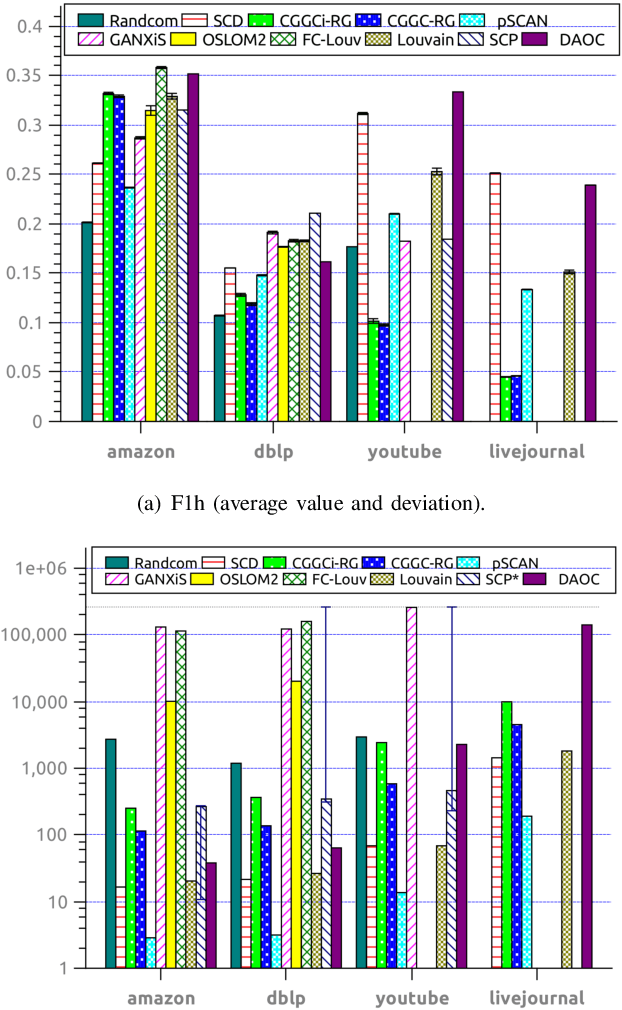
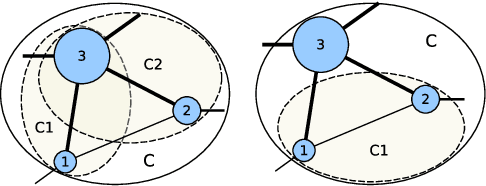
Clustering is a crucial component of many data mining systems involving the analysis and exploration of various data. Data diversity calls for clustering algorithms to be accurate while providing stable (i.e., deterministic and robust) results on arbitrary input networks. Moreover, modern systems often operate with large datasets, which implicitly constrains the complexity of the clustering algorithm. Existing clustering techniques are only partially stable, however, as they guarantee either determinism or robustness. To address this issue, we introduce DAOC, a Deterministic and Agglomerative Overlapping Clustering algorithm. DAOC leverages a new technique called Overlap Decomposition to identify fine-grained clusters in a deterministic way capturing multiple optima. In addition, it leverages a novel consensus approach, Mutual Maximal Gain, to ensure robustness and further improve the stability of the results while still being capable of identifying micro-scale clusters. Our empirical results on both synthetic and real-world networks show that DAOC yields stable clusters while being on average 25% more accurate than state-of-the-art deterministic algorithms without requiring any tuning. Our approach has the ambition to greatly simplify and speed up data analysis tasks involving iterative processing (need for determinism) as well as data fluctuations (need for robustness) and to provide accurate and reproducible results.