Categorical Representation Learning and RG flow operators for algorithmic classifiers

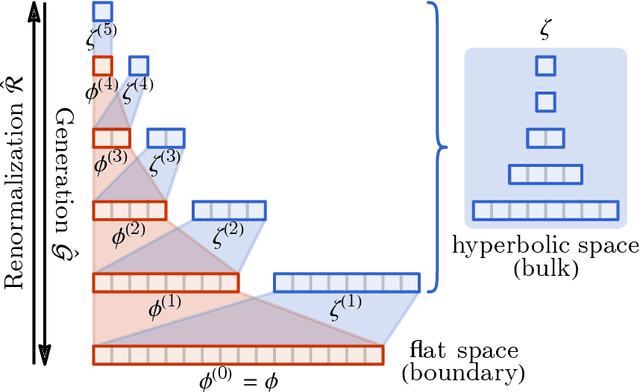
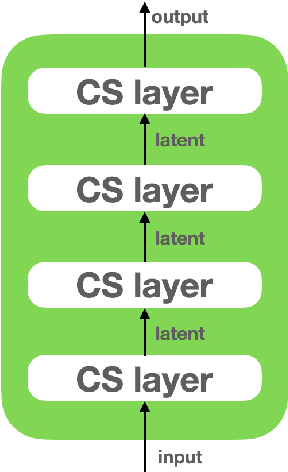
Following the earlier formalism of the categorical representation learning (arXiv:2103.14770) by the first two authors, we discuss the construction of the "RG-flow based categorifier". Borrowing ideas from theory of renormalization group flows (RG) in quantum field theory, holographic duality, and hyperbolic geometry, and mixing them with neural ODE's, we construct a new algorithmic natural language processing (NLP) architecture, called the RG-flow categorifier or for short the RG categorifier, which is capable of data classification and generation in all layers. We apply our algorithmic platform to biomedical data sets and show its performance in the field of sequence-to-function mapping. In particular we apply the RG categorifier to particular genomic sequences of flu viruses and show how our technology is capable of extracting the information from given genomic sequences, find their hidden symmetries and dominant features, classify them and use the trained data to make stochastic prediction of new plausible generated sequences associated with new set of viruses which could avoid the human immune system. The content of the current article is part of the recent US patent application submitted by first two authors (U.S. Patent Application No.: 63/313.504).

Categorical Representation Learning: Morphism is All You Need

We provide a construction for categorical representation learning and introduce the foundations of "$\textit{categorifier}$". The central theme in representation learning is the idea of $\textbf{everything to vector}$. Every object in a dataset $\mathcal{S}$ can be represented as a vector in $\mathbb{R}^n$ by an $\textit{encoding map}$ $E: \mathcal{O}bj(\mathcal{S})\to\mathbb{R}^n$. More importantly, every morphism can be represented as a matrix $E: \mathcal{H}om(\mathcal{S})\to\mathbb{R}^{n}_{n}$. The encoding map $E$ is generally modeled by a $\textit{deep neural network}$. The goal of representation learning is to design appropriate tasks on the dataset to train the encoding map (assuming that an encoding is optimal if it universally optimizes the performance on various tasks). However, the latter is still a $\textit{set-theoretic}$ approach. The goal of the current article is to promote the representation learning to a new level via a $\textit{category-theoretic}$ approach. As a proof of concept, we provide an example of a text translator equipped with our technology, showing that our categorical learning model outperforms the current deep learning models by 17 times. The content of the current article is part of the recent US patent proposal (patent application number: 63110906).