Categorical Representation Learning: Morphism is All You Need
Paper and Code
Mar 30, 2021

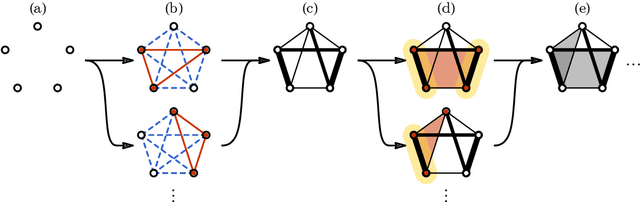

We provide a construction for categorical representation learning and introduce the foundations of "$\textit{categorifier}$". The central theme in representation learning is the idea of $\textbf{everything to vector}$. Every object in a dataset $\mathcal{S}$ can be represented as a vector in $\mathbb{R}^n$ by an $\textit{encoding map}$ $E: \mathcal{O}bj(\mathcal{S})\to\mathbb{R}^n$. More importantly, every morphism can be represented as a matrix $E: \mathcal{H}om(\mathcal{S})\to\mathbb{R}^{n}_{n}$. The encoding map $E$ is generally modeled by a $\textit{deep neural network}$. The goal of representation learning is to design appropriate tasks on the dataset to train the encoding map (assuming that an encoding is optimal if it universally optimizes the performance on various tasks). However, the latter is still a $\textit{set-theoretic}$ approach. The goal of the current article is to promote the representation learning to a new level via a $\textit{category-theoretic}$ approach. As a proof of concept, we provide an example of a text translator equipped with our technology, showing that our categorical learning model outperforms the current deep learning models by 17 times. The content of the current article is part of the recent US patent proposal (patent application number: 63110906).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge