Towards deep generation of guided wave representations for composite materials

Laminated composite materials are widely used in most fields of engineering. Wave propagation analysis plays an essential role in understanding the short-duration transient response of composite structures. The forward physics-based models are utilized to map from elastic properties space to wave propagation behavior in a laminated composite material. Due to the high-frequency, multi-modal, and dispersive nature of the guided waves, the physics-based simulations are computationally demanding. It makes property prediction, generation, and material design problems more challenging. In this work, a forward physics-based simulator such as the stiffness matrix method is utilized to collect group velocities of guided waves for a set of composite materials. A variational autoencoder (VAE)-based deep generative model is proposed for the generation of new and realistic polar group velocity representations. It is observed that the deep generator is able to reconstruct unseen representations with very low mean square reconstruction error. Global Monte Carlo and directional equally-spaced samplers are used to sample the continuous, complete and organized low-dimensional latent space of VAE. The sampled point is fed into the trained decoder to generate new polar representations. The network has shown exceptional generation capabilities. It is also seen that the latent space forms a conceptual space where different directions and regions show inherent patterns related to the generated representations and their corresponding material properties.

Inverse characterization of composites using guided waves and convolutional neural networks with dual-branch feature fusion

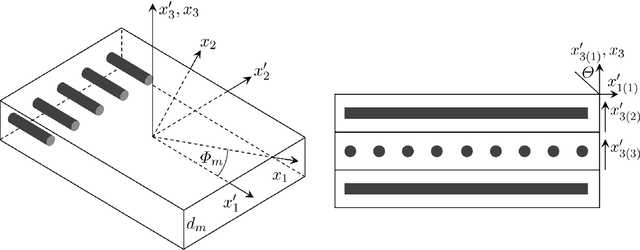
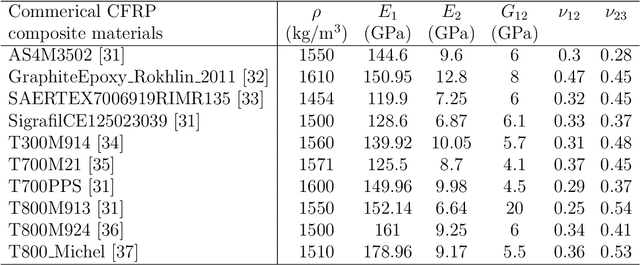
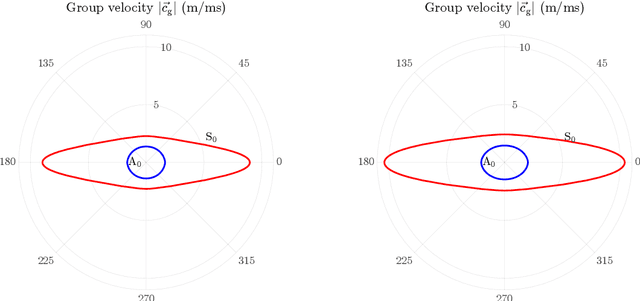
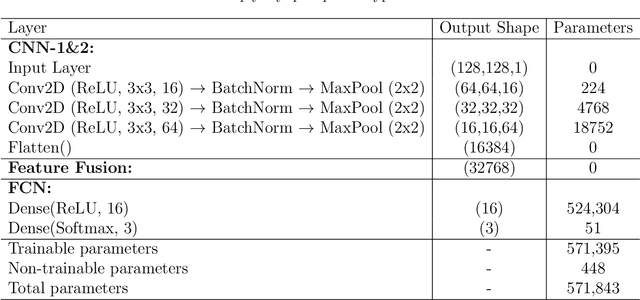
In this work, ultrasonic guided waves and a dual-branch version of convolutional neural networks are used to solve two different but related inverse problems, i.e., finding layup sequence type and identifying material properties. In the forward problem, polar group velocity representations are obtained for two fundamental Lamb wave modes using the stiffness matrix method. For the inverse problems, a supervised classification-based network is implemented to classify the polar representations into different layup sequence types (inverse problem - 1) and a regression-based network is utilized to identify the material properties (inverse problem - 2)