Anthony A. Vassiliou
Convolutional Sparse Coding Fast Approximation with Application to Seismic Reflectivity Estimation
Jun 29, 2021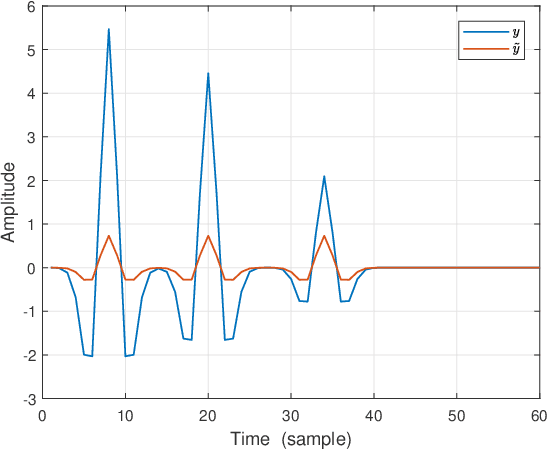
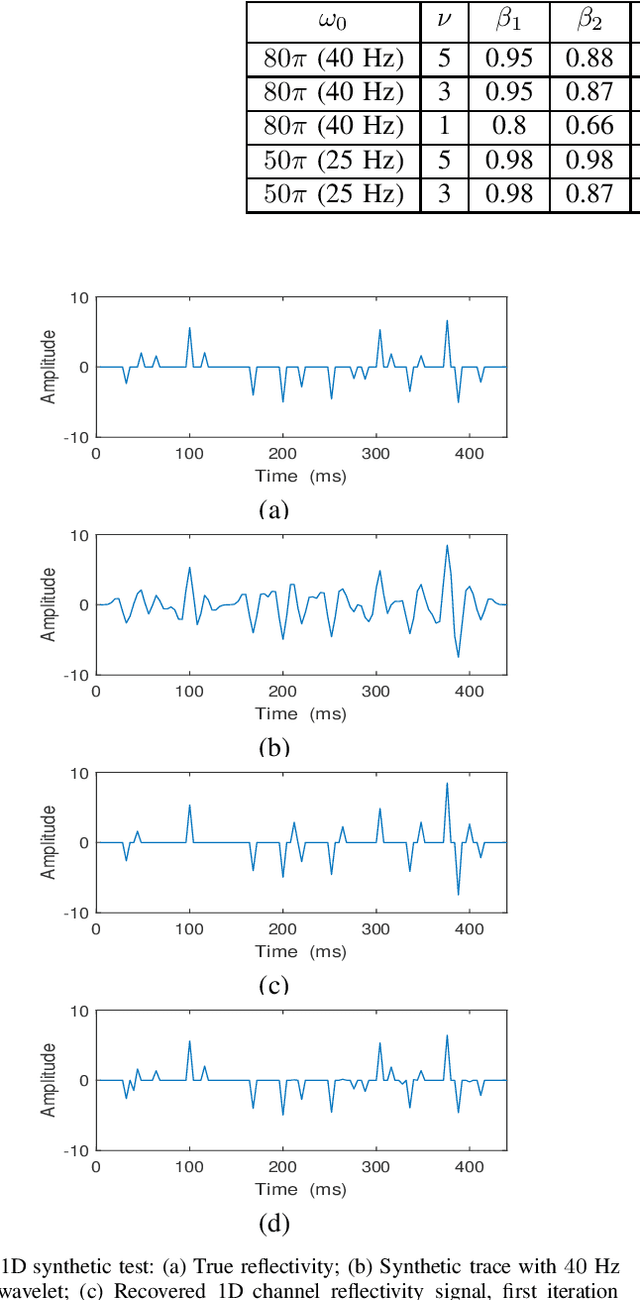
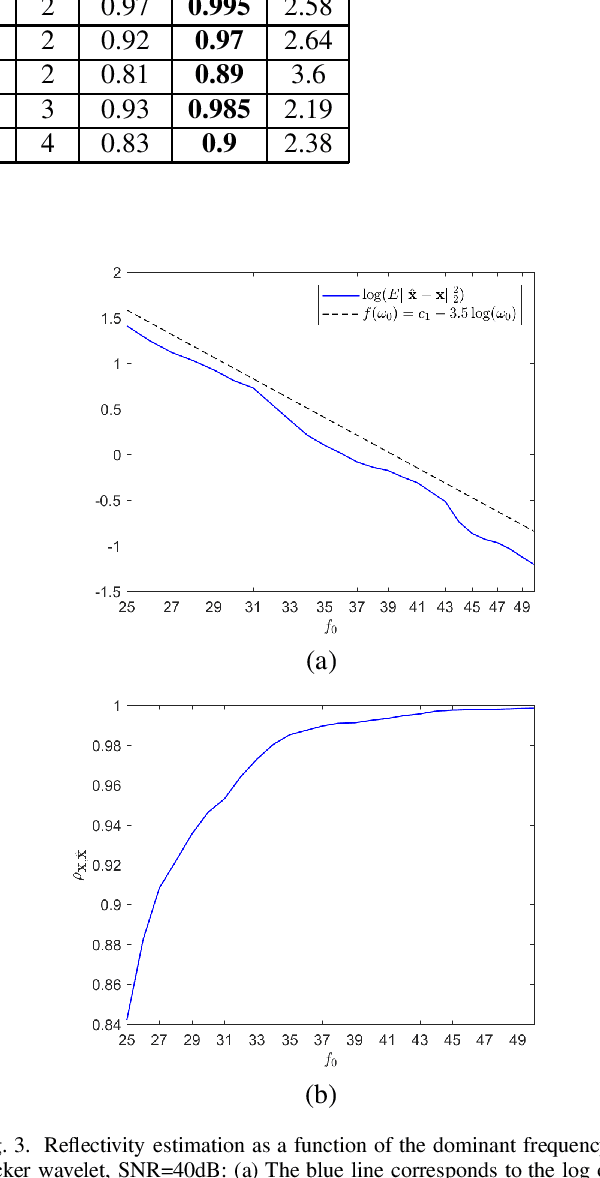
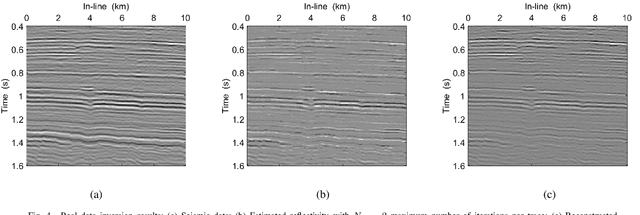
Abstract:In sparse coding, we attempt to extract features of input vectors, assuming that the data is inherently structured as a sparse superposition of basic building blocks. Similarly, neural networks perform a given task by learning features of the training data set. Recently both data-driven and model-driven feature extracting methods have become extremely popular and have achieved remarkable results. Nevertheless, practical implementations are often too slow to be employed in real-life scenarios, especially for real-time applications. We propose a speed-up upgraded version of the classic iterative thresholding algorithm, that produces a good approximation of the convolutional sparse code within 2-5 iterations. The speed advantage is gained mostly from the observation that most solvers are slowed down by inefficient global thresholding. The main idea is to normalize each data point by the local receptive field energy, before applying a threshold. This way, the natural inclination towards strong feature expressions is suppressed, so that one can rely on a global threshold that can be easily approximated, or learned during training. The proposed algorithm can be employed with a known predetermined dictionary, or with a trained dictionary. The trained version is implemented as a neural net designed as the unfolding of the proposed solver. The performance of the proposed solution is demonstrated via the seismic inversion problem in both synthetic and real data scenarios. We also provide theoretical guarantees for a stable support recovery. Namely, we prove that under certain conditions the true support is perfectly recovered within the first iteration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge