CrystalGRW: Generative Modeling of Crystal Structures with Targeted Properties via Geodesic Random Walks

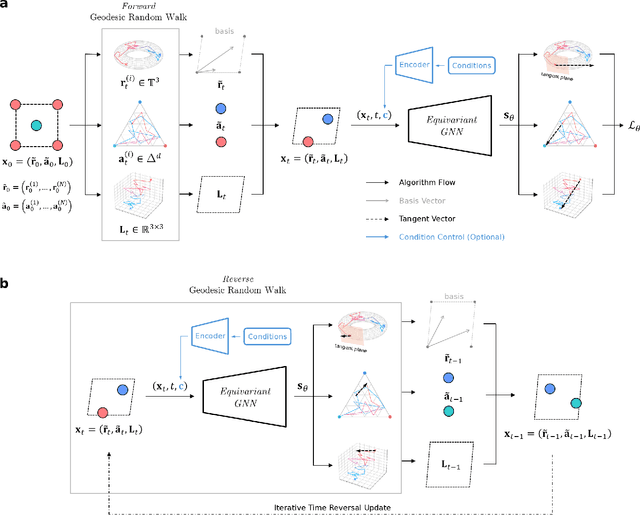
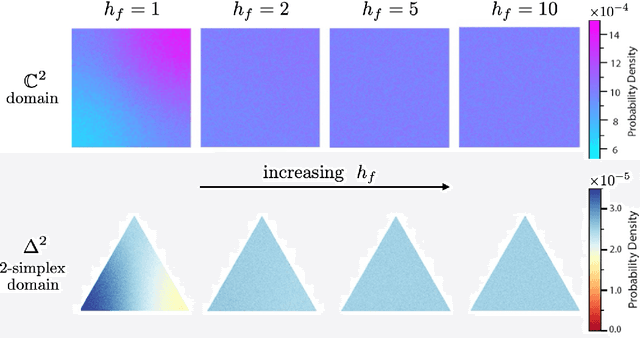
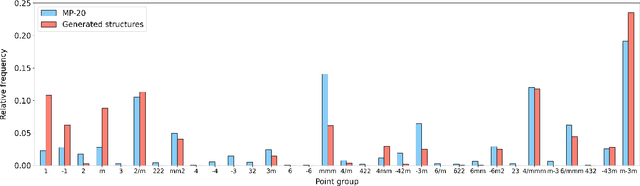
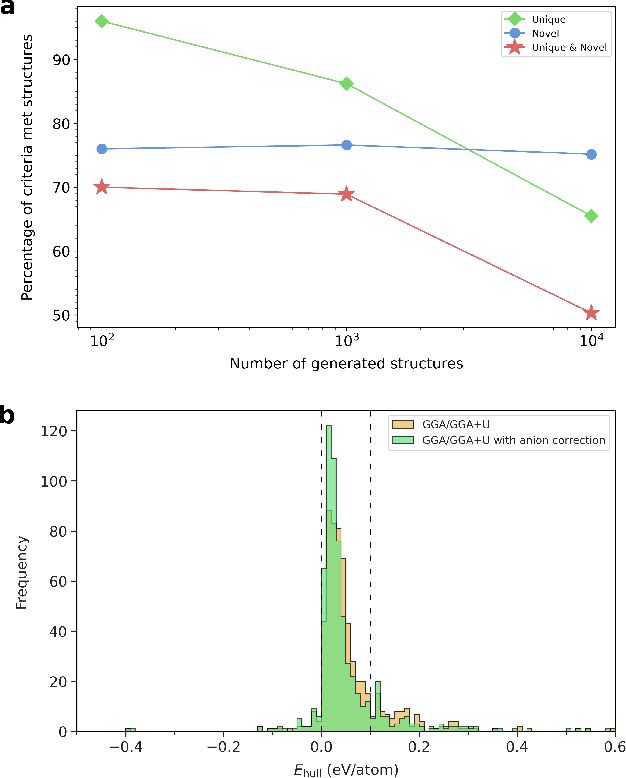
Determining whether a candidate crystalline material is thermodynamically stable depends on identifying its true ground-state structure, a central challenge in computational materials science. We introduce CrystalGRW, a diffusion-based generative model on Riemannian manifolds that proposes novel crystal configurations and can predict stable phases validated by density functional theory. The crystal properties, such as fractional coordinates, atomic types, and lattice matrices, are represented on suitable Riemannian manifolds, ensuring that new predictions generated through the diffusion process preserve the periodicity of crystal structures. We incorporate an equivariant graph neural network to also account for rotational and translational symmetries during the generation process. CrystalGRW demonstrates the ability to generate realistic crystal structures that are close to their ground states with accuracy comparable to existing models, while also enabling conditional control, such as specifying a desired crystallographic point group. These features help accelerate materials discovery and inverse design by offering stable, symmetry-consistent crystal candidates for experimental validation.

StrainNet: Predicting crystal structure elastic properties using SE(3)-equivariant graph neural networks

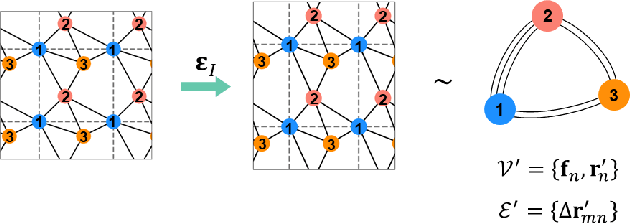
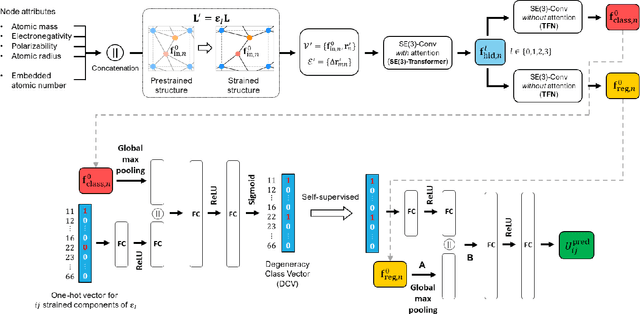
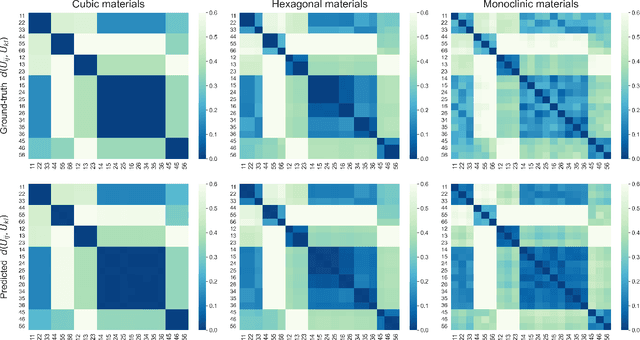
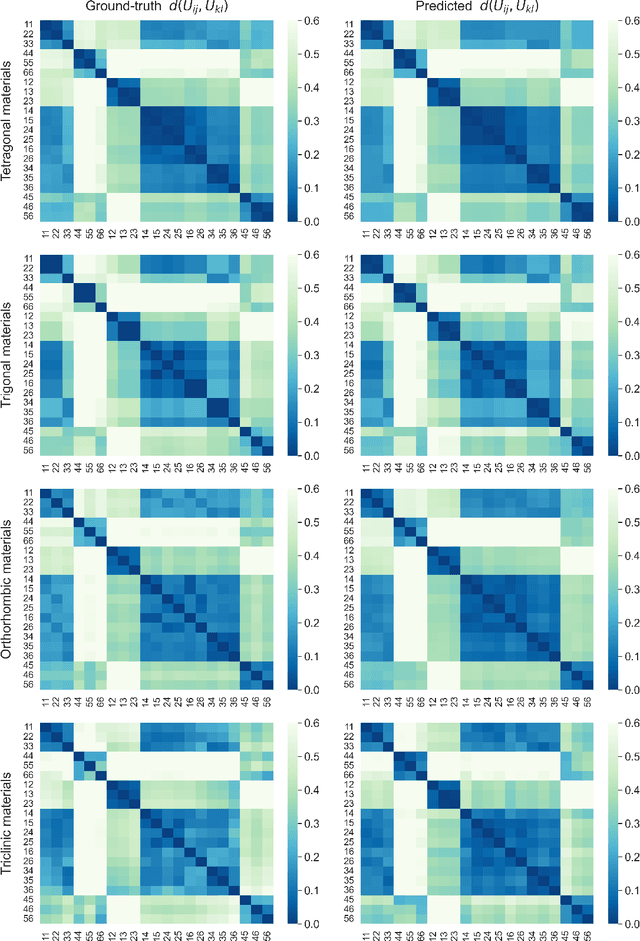
Accurately predicting the elastic properties of crystalline solids is vital for computational materials science. However, traditional atomistic scale ab initio approaches are computationally intensive, especially for studying complex materials with a large number of atoms in a unit cell. We introduce a novel data-driven approach to efficiently predict the elastic properties of crystal structures using SE(3)-equivariant graph neural networks (GNNs). This approach yields important scalar elastic moduli with the accuracy comparable to recent data-driven studies. Importantly, our symmetry-aware GNNs model also enables the prediction of the strain energy density (SED) and the associated elastic constants, the fundamental tensorial quantities that are significantly influenced by a material's crystallographic group. The model consistently distinguishes independent elements of SED tensors, in accordance with the symmetry of the crystal structures. Finally, our deep learning model possesses meaningful latent features, offering an interpretable prediction of the elastic properties.