Anne Draelos
Bubblewrap: Online tiling and real-time flow prediction on neural manifolds
Aug 31, 2021



Abstract:While most classic studies of function in experimental neuroscience have focused on the coding properties of individual neurons, recent developments in recording technologies have resulted in an increasing emphasis on the dynamics of neural populations. This has given rise to a wide variety of models for analyzing population activity in relation to experimental variables, but direct testing of many neural population hypotheses requires intervening in the system based on current neural state, necessitating models capable of inferring neural state online. Existing approaches, primarily based on dynamical systems, require strong parametric assumptions that are easily violated in the noise-dominated regime and do not scale well to the thousands of data channels in modern experiments. To address this problem, we propose a method that combines fast, stable dimensionality reduction with a soft tiling of the resulting neural manifold, allowing dynamics to be approximated as a probability flow between tiles. This method can be fit efficiently using online expectation maximization, scales to tens of thousands of tiles, and outperforms existing methods when dynamics are noise-dominated or feature multi-modal transition probabilities. The resulting model can be trained at kiloHertz data rates, produces accurate approximations of neural dynamics within minutes, and generates predictions on submillisecond time scales. It retains predictive performance throughout many time steps into the future and is fast enough to serve as a component of closed-loop causal experiments.
Online Neural Connectivity Estimation with Noisy Group Testing
Jul 27, 2020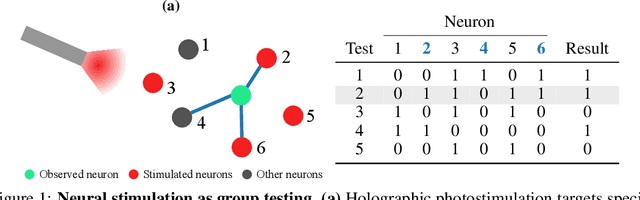
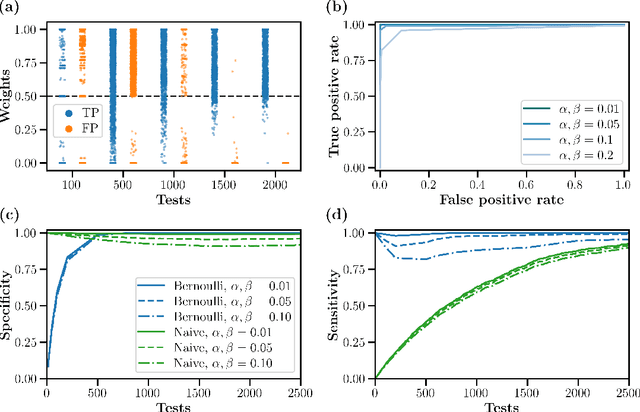
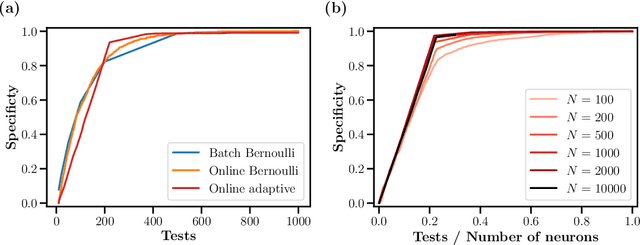
Abstract:One of the primary goals of systems neuroscience is to relate the structure of neural circuits to their function, yet patterns of connectivity are difficult to establish when recording from large populations in behaving organisms. Many previous approaches have attempted to estimate functional connectivity between neurons using statistical modeling of observational data, but these approaches rely heavily on parametric assumptions and are purely correlational. Recently, however, holographic photostimulation techniques have made it possible to precisely target selected ensembles of neurons, offering the possibility of establishing direct causal links. A naive method for inferring functional connections is to stimulate each individual neuron multiple times and observe the responses of cells in the local network, but this approach scales poorly with the number of neurons. Here, we propose a method based on noisy group testing that drastically increases the efficiency of this process in sparse networks. By stimulating small ensembles of neurons, we show that it is possible to recover binarized network connectivity with a number of tests that grows only logarithmically with population size under minimal statistical assumptions. Moreover, we prove that our approach, which reduces to an efficiently solvable convex optimization problem, is equivalent to Variational Bayesian inference on the binary connection weights, and we derive rigorous bounds on the posterior marginals. This allows us to extend our method to the streaming setting, where continuously updated posteriors allow for optional stopping, and we demonstrate the feasibility of inferring connectivity for networks of up to tens of thousands of neurons online.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge