Transfer Entropy in Graph Convolutional Neural Networks

Graph Convolutional Networks (GCN) are Graph Neural Networks where the convolutions are applied over a graph. In contrast to Convolutional Neural Networks, GCN's are designed to perform inference on graphs, where the number of nodes can vary, and the nodes are unordered. In this study, we address two important challenges related to GCNs: i) oversmoothing; and ii) the utilization of node relational properties (i.e., heterophily and homophily). Oversmoothing is the degradation of the discriminative capacity of nodes as a result of repeated aggregations. Heterophily is the tendency for nodes of different classes to connect, whereas homophily is the tendency of similar nodes to connect. We propose a new strategy for addressing these challenges in GCNs based on Transfer Entropy (TE), which measures of the amount of directed transfer of information between two time varying nodes. Our findings indicate that using node heterophily and degree information as a node selection mechanism, along with feature-based TE calculations, enhances accuracy across various GCN models. Our model can be easily modified to improve classification accuracy of a GCN model. As a trade off, this performance boost comes with a significant computational overhead when the TE is computed for many graph nodes.

Learning in Convolutional Neural Networks Accelerated by Transfer Entropy

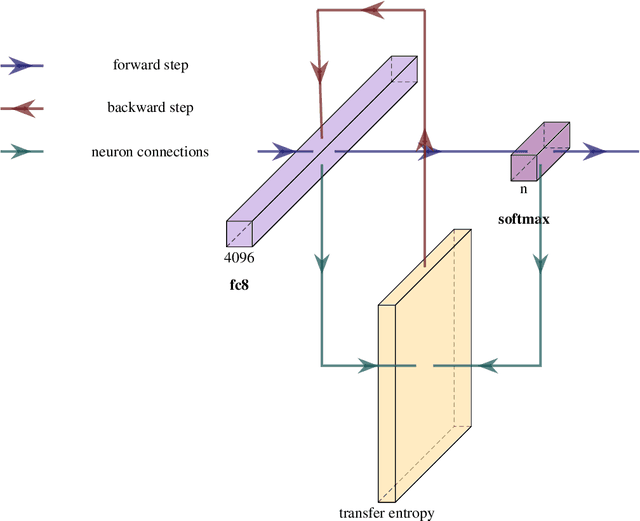
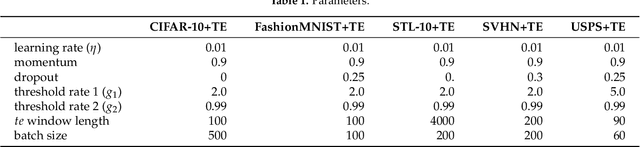
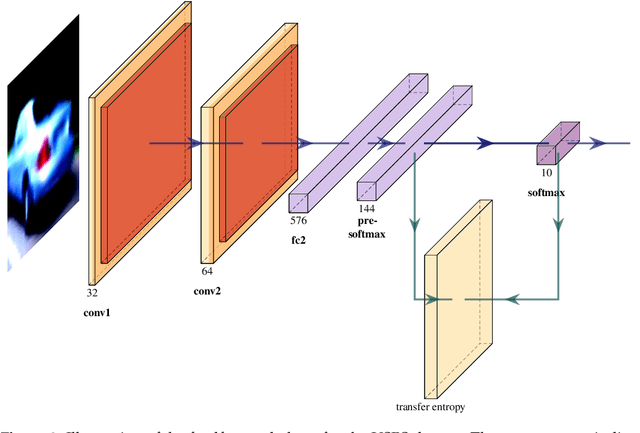
Recently, there is a growing interest in applying Transfer Entropy (TE) in quantifying the effective connectivity between artificial neurons. In a feedforward network, the TE can be used to quantify the relationships between neuron output pairs located in different layers. Our focus is on how to include the TE in the learning mechanisms of a Convolutional Neural Network (CNN) architecture. We introduce a novel training mechanism for CNN architectures which integrates the TE feedback connections. Adding the TE feedback parameter accelerates the training process, as fewer epochs are needed. On the flip side, it adds computational overhead to each epoch. According to our experiments on CNN classifiers, to achieve a reasonable computational overhead--accuracy trade-off, it is efficient to consider only the inter-neural information transfer of a random subset of the neuron pairs from the last two fully connected layers. The TE acts as a smoothing factor, generating stability and becoming active only periodically, not after processing each input sample. Therefore, we can consider the TE is in our model a slowly changing meta-parameter.

Learning in Feedforward Neural Networks Accelerated by Transfer Entropy

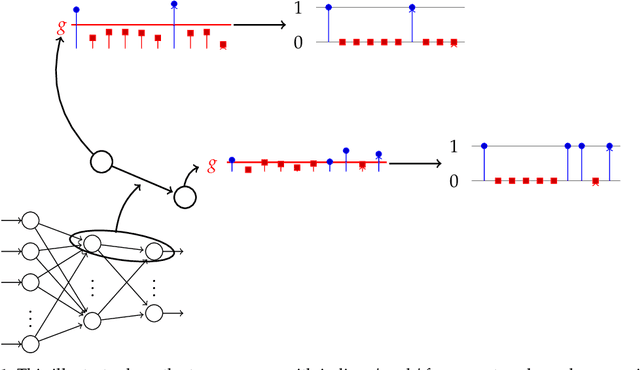
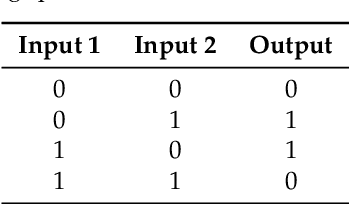
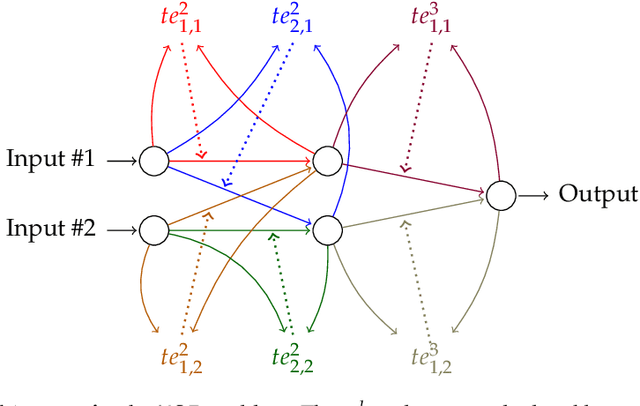
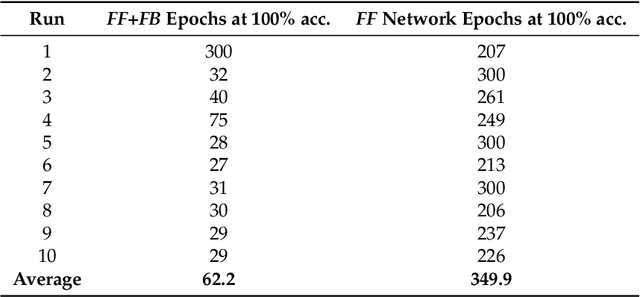
Current neural networks architectures are many times harder to train because of the increasing size and complexity of the used datasets. Our objective is to design more efficient training algorithms utilizing causal relationships inferred from neural networks. The transfer entropy (TE) was initially introduced as an information transfer measure used to quantify the statistical coherence between events (time series). Later, it was related to causality, even if they are not the same. There are only few papers reporting applications of causality or TE in neural networks. Our contribution is an information-theoretical method for analyzing information transfer between the nodes of feedforward neural networks. The information transfer is measured by the TE of feedback neural connections. Intuitively, TE measures the relevance of a connection in the network and the feedback amplifies this connection. We introduce a backpropagation type training algorithm that uses TE feedback connections to improve its performance.