Quantum machine learning channel discrimination

In the problem of quantum channel discrimination, one distinguishes between a given number of quantum channels, which is done by sending an input state through a channel and measuring the output state. This work studies applications of variational quantum circuits and machine learning techniques for discriminating such channels. In particular, we explore (i) the practical implementation of embedding this task into the framework of variational quantum computing, (ii) training a quantum classifier based on variational quantum circuits, and (iii) applying the quantum kernel estimation technique. For testing these three channel discrimination approaches, we considered a pair of entanglement-breaking channels and the depolarizing channel with two different depolarization factors. For the approach (i), we address solving the quantum channel discrimination problem using widely discussed parallel and sequential strategies. We show the advantage of the latter in terms of better convergence with less quantum resources. Quantum channel discrimination with a variational quantum classifier (ii) allows one to operate even with random and mixed input states and simple variational circuits. The kernel-based classification approach (iii) is also found effective as it allows one to discriminate depolarizing channels associated not with just fixed values of the depolarization factor, but with ranges of it. Additionally, we discovered that a simple modification of one of the commonly used kernels significantly increases the efficiency of this approach. Finally, our numerical findings reveal that the performance of variational methods of channel discrimination depends on the trace of the product of the output states. These findings demonstrate that quantum machine learning can be used to discriminate channels, such as those representing physical noise processes.

Self-learning eigenstates with a quantum processor

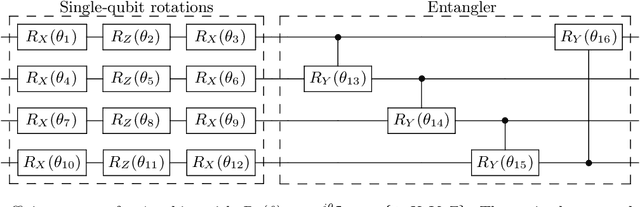
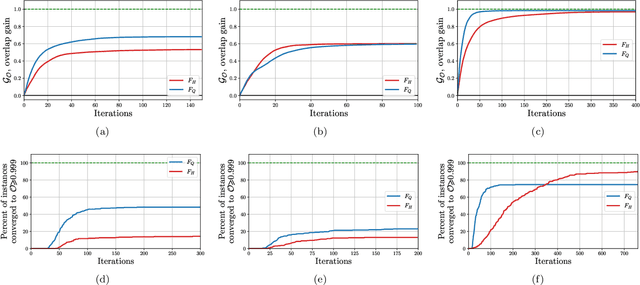
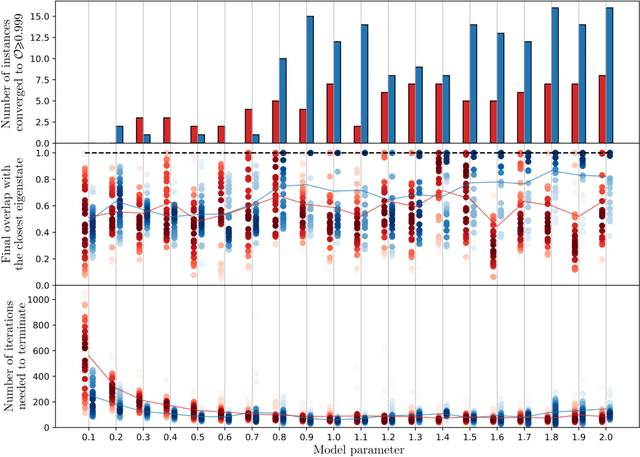
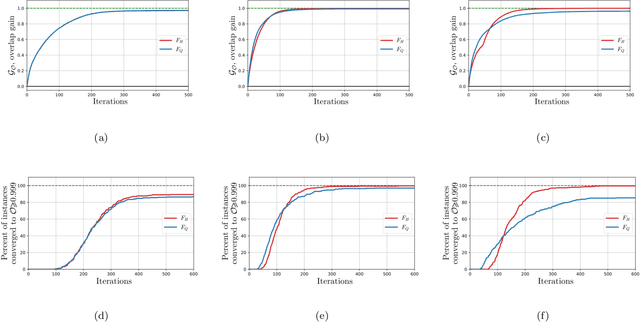
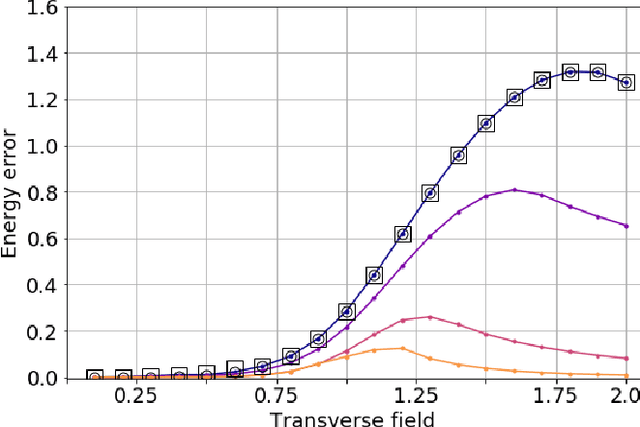
Solutions to many-body problem instances often involve an intractable number of degrees of freedom and admit no known approximations in general form. In practice, representing quantum-mechanical states of a given Hamiltonian using available numerical methods, in particular those based on variational Monte Carlo simulations, become exponentially more challenging with increasing system size. Recently quantum algorithms implemented as variational models, have been proposed to accelerate such simulations. The variational ansatz states are characterized by a polynomial number of parameters devised in a way to minimize the expectation value of a given Hamiltonian, which is emulated by local measurements. In this study, we develop a means to certify the termination of variational algorithms. We demonstrate our approach by applying it to three models: the transverse field Ising model, the model of one-dimensional spinless fermions with competing interactions and the Schwinger model of quantum electrodynamics. By means of comparison, we observe that our approach shows better performance near critical points in these models. We hence take a further step to improve the applicability and to certify the results of variational quantum simulators.

Machine Learning Phase Transitions with a Quantum Processor

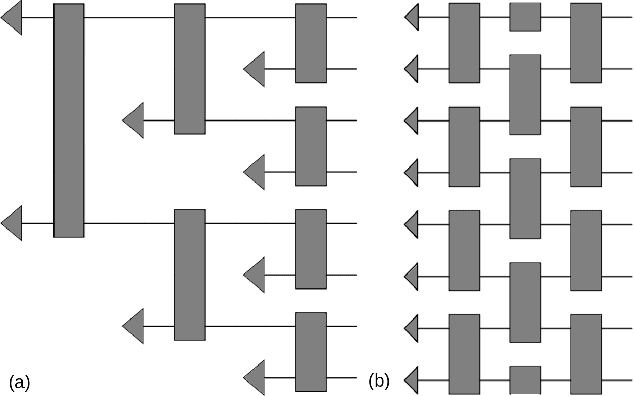
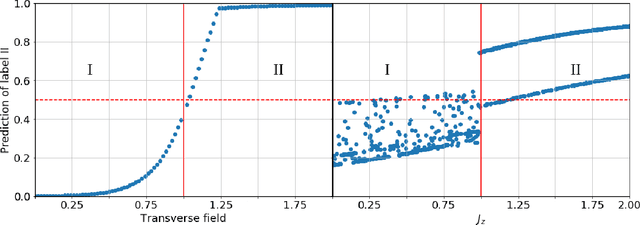
Machine learning has emerged as a promising approach to study the properties of many-body systems. Recently proposed as a tool to classify phases of matter, the approach relies on classical simulation methods$-$such as Monte Carlo$-$which are known to experience an exponential slowdown when simulating certain quantum systems. To overcome this slowdown while still leveraging machine learning, we propose a variational quantum algorithm which merges quantum simulation and quantum machine learning to classify phases of matter. Our classifier is directly fed labeled states recovered by the variational quantum eigensolver algorithm, thereby avoiding the data reading slowdown experienced in many applications of quantum enhanced machine learning. We propose families of variational ansatz states that are inspired directly by tensor networks. This allows us to use tools from tensor network theory to explain properties of the phase diagrams the presented method recovers. Finally, we propose a nearest-neighbour (checkerboard) quantum neural network. This majority vote quantum classifier is successfully trained to recognize phases of matter with $99\%$ accuracy for the transverse field Ising model and $94\%$ accuracy for the XXZ model. These findings suggest that our merger between quantum simulation and quantum enhanced machine learning offers a fertile ground to develop computational insights into quantum systems.