Rapid quantification of COVID-19 pneumonia burden from computed tomography with convolutional LSTM networks

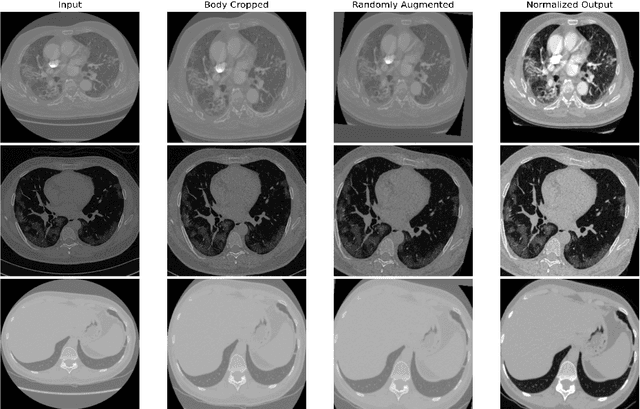
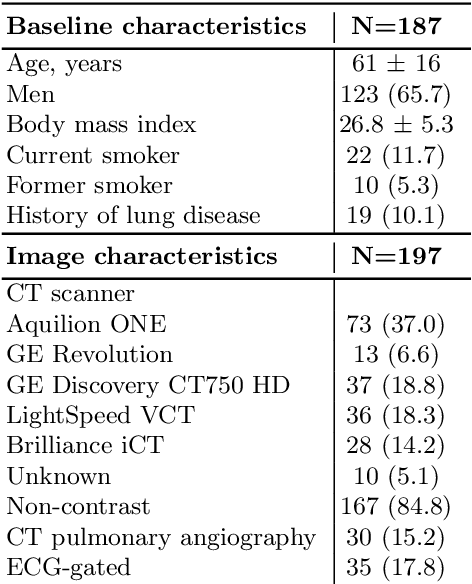
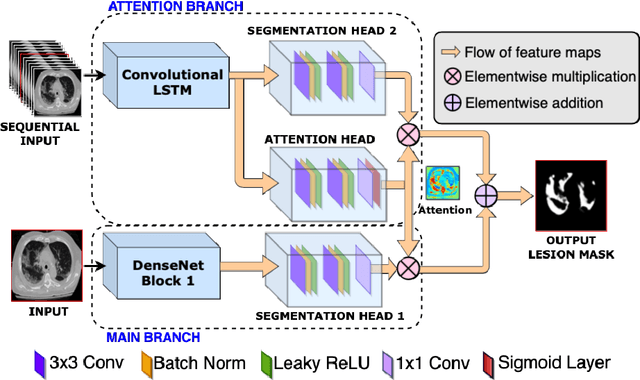
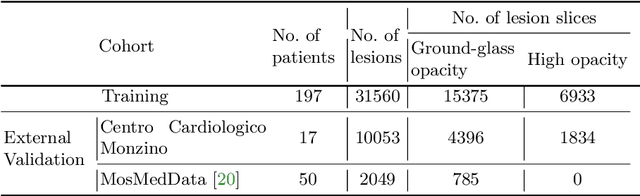
Quantitative lung measures derived from computed tomography (CT) have been demonstrated to improve prognostication in coronavirus disease (COVID-19) patients, but are not part of the clinical routine since required manual segmentation of lung lesions is prohibitively time-consuming. We propose a new fully automated deep learning framework for rapid quantification and differentiation between lung lesions in COVID-19 pneumonia from both contrast and non-contrast CT images using convolutional Long Short-Term Memory (ConvLSTM) networks. Utilizing the expert annotations, model training was performed 5 times with separate hold-out sets using 5-fold cross-validation to segment ground-glass opacity and high opacity (including consolidation and pleural effusion). The performance of the method was evaluated on CT data sets from 197 patients with positive reverse transcription polymerase chain reaction test result for SARS-CoV-2. Strong agreement between expert manual and automatic segmentation was obtained for lung lesions with a Dice score coefficient of 0.876 $\pm$ 0.005; excellent correlations of 0.978 and 0.981 for ground-glass opacity and high opacity volumes. In the external validation set of 67 patients, there was dice score coefficient of 0.767 $\pm$ 0.009 as well as excellent correlations of 0.989 and 0.996 for ground-glass opacity and high opacity volumes. Computations for a CT scan comprising 120 slices were performed under 2 seconds on a personal computer equipped with NVIDIA Titan RTX graphics processing unit. Therefore, our deep learning-based method allows rapid fully-automated quantitative measurement of pneumonia burden from CT and may generate results with an accuracy similar to the expert readers.

The Complexity of Manipulating $k$-Approval Elections

An important problem in computational social choice theory is the complexity of undesirable behavior among agents, such as control, manipulation, and bribery in election systems. These kinds of voting strategies are often tempting at the individual level but disastrous for the agents as a whole. Creating election systems where the determination of such strategies is difficult is thus an important goal. An interesting set of elections is that of scoring protocols. Previous work in this area has demonstrated the complexity of misuse in cases involving a fixed number of candidates, and of specific election systems on unbounded number of candidates such as Borda. In contrast, we take the first step in generalizing the results of computational complexity of election misuse to cases of infinitely many scoring protocols on an unbounded number of candidates. Interesting families of systems include $k$-approval and $k$-veto elections, in which voters distinguish $k$ candidates from the candidate set. Our main result is to partition the problems of these families based on their complexity. We do so by showing they are polynomial-time computable, NP-hard, or polynomial-time equivalent to another problem of interest. We also demonstrate a surprising connection between manipulation in election systems and some graph theory problems.