Hyperbolic Machine Learning Moment Closures for the BGK Equations

We introduce a hyperbolic closure for the Grad moment expansion of the Bhatnagar-Gross-Krook's (BGK) kinetic model using a neural network (NN) trained on BGK's moment data. This closure is motivated by the exact closure for the free streaming limit that we derived in our paper on closures in transport \cite{Huang2022-RTE1}. The exact closure relates the gradient of the highest moment to the gradient of four lower moments. As with our past work, the model presented here learns the gradient of the highest moment in terms of the coefficients of gradients for all lower ones. By necessity, this means that the resulting hyperbolic system is not conservative in the highest moment. For stability, the output layers of the NN are designed to enforce hyperbolicity and Galilean invariance. This ensures the model can be run outside of the training window of the NN. Unlike our previous work on radiation transport that dealt with linear models, the BGK model's nonlinearity demanded advanced training tools. These comprised an optimal learning rate discovery, one cycle training, batch normalization in each neural layer, and the use of the \texttt{AdamW} optimizer. To address the non-conservative structure of the hyperbolic model, we adopt the FORCE numerical method to achieve robust solutions. This results in a comprehensive computing model combining learned closures with methods for solving hyperbolic models. The proposed model can capture accurate moment solutions across a broad spectrum of Knudsen numbers. Our paper details the multi-scale model construction and is run on a range of test problems.

Machine learning moment closure models for the radiative transfer equation III: enforcing hyperbolicity and physical characteristic speeds

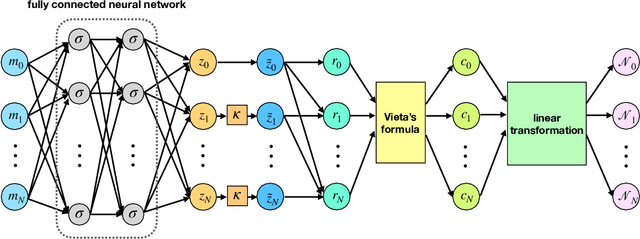
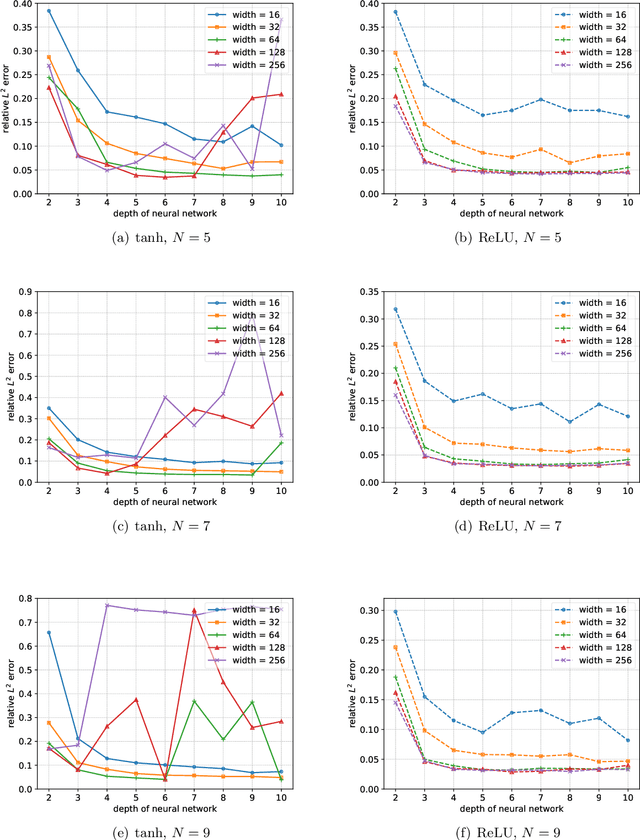
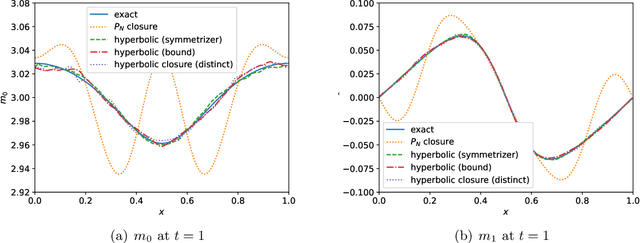
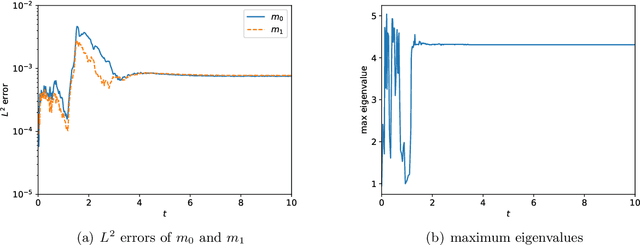
This is the third paper in a series in which we develop machine learning (ML) moment closure models for the radiative transfer equation (RTE). In our previous work \cite{huang2021gradient}, we proposed an approach to learn the gradient of the unclosed high order moment, which performs much better than learning the moment itself and the conventional $P_N$ closure. However, while the ML moment closure has better accuracy, it is not able to guarantee hyperbolicity and has issues with long time stability. In our second paper \cite{huang2021hyperbolic}, we identified a symmetrizer which leads to conditions that enforce that the gradient based ML closure is symmetrizable hyperbolic and stable over long time. The limitation of this approach is that in practice the highest moment can only be related to four, or fewer, lower moments. In this paper, we propose a new method to enforce the hyperbolicity of the ML closure model. Motivated by the observation that the coefficient matrix of the closure system is a lower Hessenberg matrix, we relate its eigenvalues to the roots of an associated polynomial. We design two new neural network architectures based on this relation. The ML closure model resulting from the first neural network is weakly hyperbolic and guarantees the physical characteristic speeds, i.e., the eigenvalues are bounded by the speed of light. The second model is strictly hyperbolic and does not guarantee the boundedness of the eigenvalues. Several benchmark tests including the Gaussian source problem and the two-material problem show the good accuracy, stability and generalizability of our hyperbolic ML closure model.

Machine learning moment closure models for the radiative transfer equation II: enforcing global hyperbolicity in gradient based closures

This is the second paper in a series in which we develop machine learning (ML) moment closure models for the radiative transfer equation (RTE). In our previous work \cite{huang2021gradient}, we proposed an approach to directly learn the gradient of the unclosed high order moment, which performs much better than learning the moment itself and the conventional $P_N$ closure. However, the ML moment closure model in \cite{huang2021gradient} is not able to guarantee hyperbolicity and long time stability. We propose in this paper a method to enforce the global hyperbolicity of the ML closure model. The main idea is to seek a symmetrizer (a symmetric positive definite matrix) for the closure system, and derive constraints such that the system is globally symmetrizable hyperbolic. It is shown that the new ML closure system inherits the dissipativeness of the RTE and preserves the correct diffusion limit as the Knunsden number goes to zero. Several benchmark tests including the Gaussian source problem and the two-material problem show the good accuracy, long time stability and generalizability of our globally hyperbolic ML closure model.

Machine learning moment closure models for the radiative transfer equation I: directly learning a gradient based closure

In this paper, we take a data-driven approach and apply machine learning to the moment closure problem for radiative transfer equation in slab geometry. Instead of learning the unclosed high order moment, we propose to directly learn the gradient of the high order moment using neural networks. This new approach is consistent with the exact closure we derive for the free streaming limit and also provides a natural output normalization. A variety of benchmark tests, including the variable scattering problem, the Gaussian source problem and the two material problem, show both good accuracy and generalizability of our machine learning closure model.