Estimating prediction error for complex samples

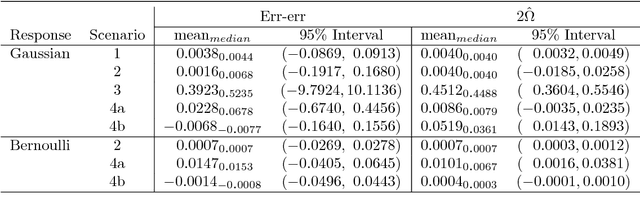
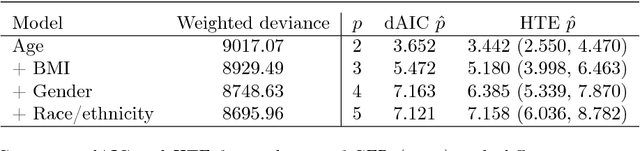
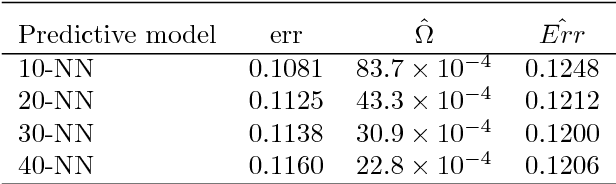
Non-uniform random samples are commonly generated in multiple scientific fields ranging from economics to medicine. Complex sampling designs afford research with increased precision for estimating parameters of interest in less prevalent sub-populations. With a growing interest in using complex samples to generate prediction models for numerous outcomes it is necessary to account for the sampling design that gave rise to the data in order to assess the generalized predictive utility of a proposed prediction rule. Specifically, after learning a prediction rule based on a complex sample, it is of interest to estimate the rule's error rate when applied to unobserved members of the population. Efron proposed a general class of covariance-inflated prediction error estimators that assumed the available training data is representative of the target population for which the prediction rule is to be applied. We extend Efron's estimator to the complex sample context by incorporating Horvitz-Thompson sampling weights and show that it is consistent for the true generalization error rate when applied to the underlying superpopulation giving rise to the training sample. The resulting Horvitz-Thompson-Efron (HTE) estimator is equivalent to dAIC---a recent extension of AIC to survey sampling data---and is more widely applicable. The proposed methodology is assessed via empirical simulations and is applied to data predicting renal function that was obtained from the National Health and Nutrition Examination Survey (NHANES).

Bayesian Inference on Matrix Manifolds for Linear Dimensionality Reduction

We reframe linear dimensionality reduction as a problem of Bayesian inference on matrix manifolds. This natural paradigm extends the Bayesian framework to dimensionality reduction tasks in higher dimensions with simpler models at greater speeds. Here an orthogonal basis is treated as a single point on a manifold and is associated with a linear subspace on which observations vary maximally. Throughout this paper, we employ the Grassmann and Stiefel manifolds for various dimensionality reduction problems, explore the connection between the two manifolds, and use Hybrid Monte Carlo for posterior sampling on the Grassmannian for the first time. We delineate in which situations either manifold should be considered. Further, matrix manifold models are used to yield scientific insight in the context of cognitive neuroscience, and we conclude that our methods are suitable for basic inference as well as accurate prediction.