Necessary Conditions for Discontinuities of Multidimensional Size Functions

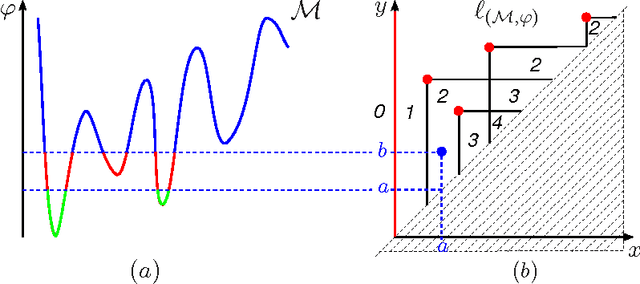
Some new results about multidimensional Topological Persistence are presented, proving that the discontinuity points of a k-dimensional size function are necessarily related to the pseudocritical or special values of the associated measuring function.

Stability in multidimensional Size Theory

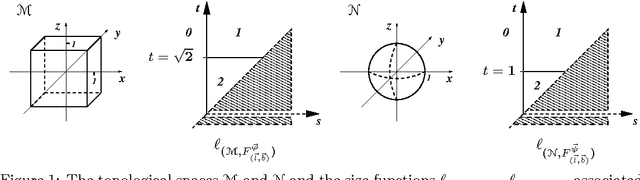
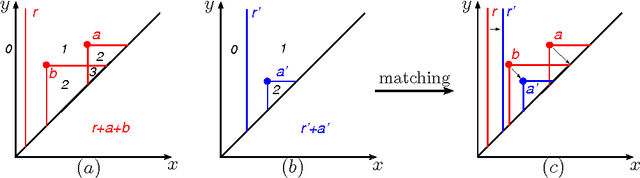
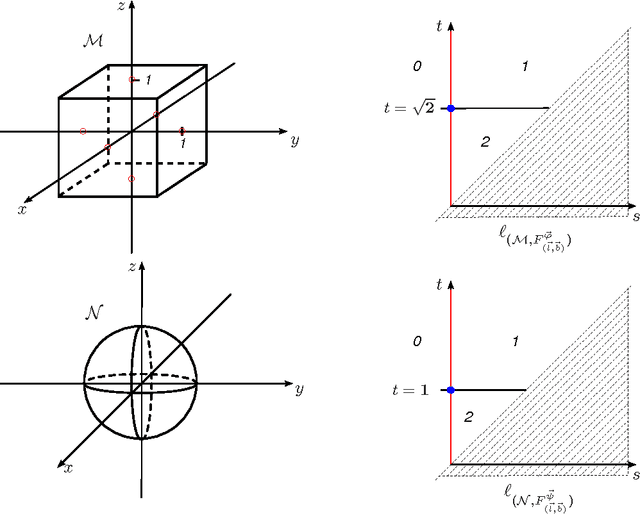
This paper proves that in Size Theory the comparison of multidimensional size functions can be reduced to the 1-dimensional case by a suitable change of variables. Indeed, we show that a foliation in half-planes can be given, such that the restriction of a multidimensional size function to each of these half-planes turns out to be a classical size function in two scalar variables. This leads to the definition of a new distance between multidimensional size functions, and to the proof of their stability with respect to that distance.