Evaluating Meta-Feature Selection for the Algorithm Recommendation Problem

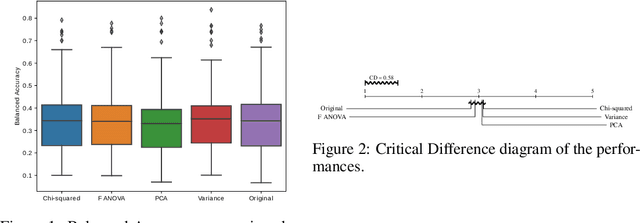
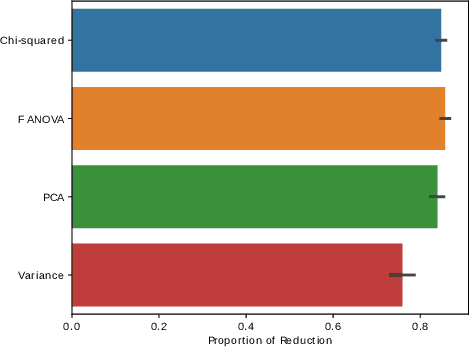
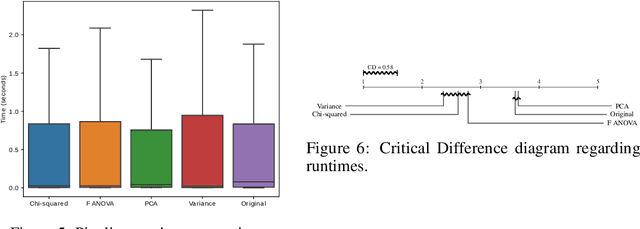
With the popularity of Machine Learning (ML) solutions, algorithms and data have been released faster than the capacity of processing them. In this context, the problem of Algorithm Recommendation (AR) is receiving a significant deal of attention recently. This problem has been addressed in the literature as a learning task, often as a Meta-Learning problem where the aim is to recommend the best alternative for a specific dataset. For such, datasets encoded by meta-features are explored by ML algorithms that try to learn the mapping between meta-representations and the best technique to be used. One of the challenges for the successful use of ML is to define which features are the most valuable for a specific dataset since several meta-features can be used, which increases the meta-feature dimension. This paper presents an empirical analysis of Feature Selection and Feature Extraction in the meta-level for the AR problem. The present study was focused on three criteria: predictive performance, dimensionality reduction, and pipeline runtime. As we verified, applying Dimensionality Reduction (DR) methods did not improve predictive performances in general. However, DR solutions reduced about 80% of the meta-features, obtaining pretty much the same performance as the original setup but with lower runtimes. The only exception was PCA, which presented about the same runtime as the original meta-features. Experimental results also showed that various datasets have many non-informative meta-features and that it is possible to obtain high predictive performance using around 20% of the original meta-features. Therefore, due to their natural trend for high dimensionality, DR methods should be used for Meta-Feature Selection and Meta-Feature Extraction.

Using dynamical quantization to perform split attempts in online tree regressors

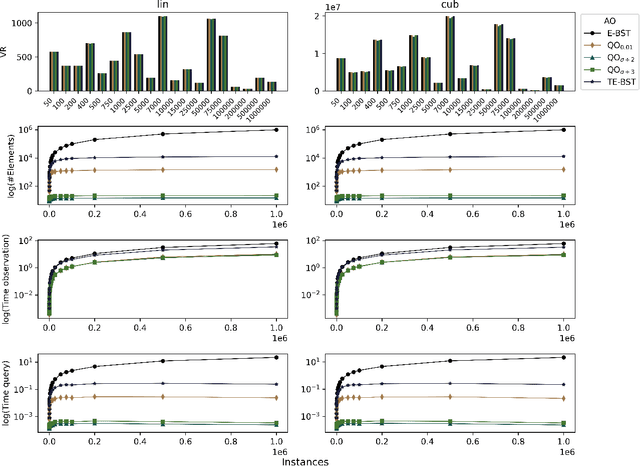
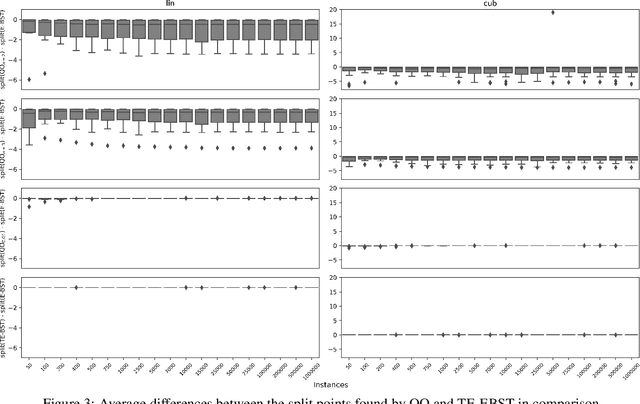
A central aspect of online decision tree solutions is evaluating the incoming data and enabling model growth. For such, trees much deal with different kinds of input features and partition them to learn from the data. Numerical features are no exception, and they pose additional challenges compared to other kinds of features, as there is no trivial strategy to choose the best point to make a split decision. The problem is even more challenging in regression tasks because both the features and the target are continuous. Typical online solutions evaluate and store all the points monitored between split attempts, which goes against the constraints posed in real-time applications. In this paper, we introduce the Quantization Observer (QO), a simple yet effective hashing-based algorithm to monitor and evaluate split point candidates in numerical features for online tree regressors. QO can be easily integrated into incremental decision trees, such as Hoeffding Trees, and it has a monitoring cost of $O(1)$ per instance and sub-linear cost to evaluate split candidates. Previous solutions had a $O(\log n)$ cost per insertion (in the best case) and a linear cost to evaluate split points. Our extensive experimental setup highlights QO's effectiveness in providing accurate split point suggestions while spending much less memory and processing time than its competitors.