Anass Aghbalou
Sharp error bounds for imbalanced classification: how many examples in the minority class?
Oct 23, 2023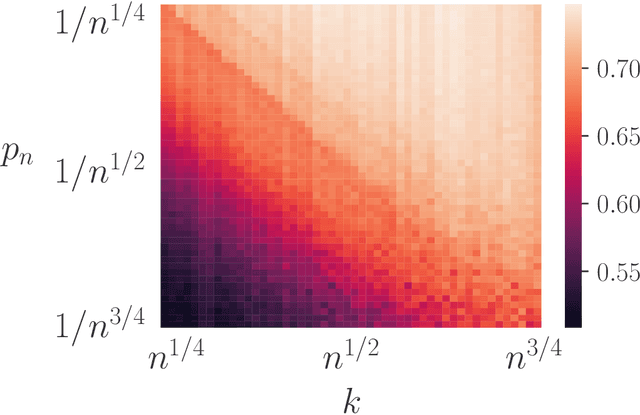
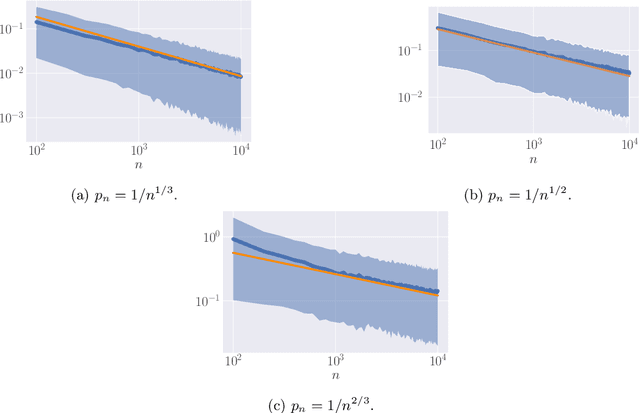
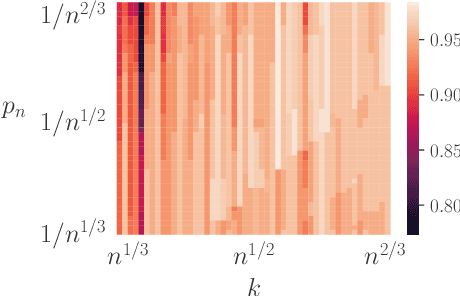
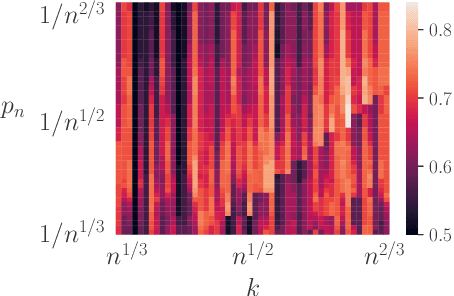
Abstract:When dealing with imbalanced classification data, reweighting the loss function is a standard procedure allowing to equilibrate between the true positive and true negative rates within the risk measure. Despite significant theoretical work in this area, existing results do not adequately address a main challenge within the imbalanced classification framework, which is the negligible size of one class in relation to the full sample size and the need to rescale the risk function by a probability tending to zero. To address this gap, we present two novel contributions in the setting where the rare class probability approaches zero: (1) a non asymptotic fast rate probability bound for constrained balanced empirical risk minimization, and (2) a consistent upper bound for balanced nearest neighbors estimates. Our findings provide a clearer understanding of the benefits of class-weighting in realistic settings, opening new avenues for further research in this field.
Hypothesis Transfer Learning with Surrogate Classification Losses
May 31, 2023Abstract:Hypothesis transfer learning (HTL) contrasts domain adaptation by allowing for a previous task leverage, named the source, into a new one, the target, without requiring access to the source data. Indeed, HTL relies only on a hypothesis learnt from such source data, relieving the hurdle of expansive data storage and providing great practical benefits. Hence, HTL is highly beneficial for real-world applications relying on big data. The analysis of such a method from a theoretical perspective faces multiple challenges, particularly in classification tasks. This paper deals with this problem by studying the learning theory of HTL through algorithmic stability, an attractive theoretical framework for machine learning algorithms analysis. In particular, we are interested in the statistical behaviour of the regularized empirical risk minimizers in the case of binary classification. Our stability analysis provides learning guarantees under mild assumptions. Consequently, we derive several complexity-free generalization bounds for essential statistical quantities like the training error, the excess risk and cross-validation estimates. These refined bounds allow understanding the benefits of transfer learning and comparing the behaviour of standard losses in different scenarios, leading to valuable insights for practitioners.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge