Ananthanarayanan Chockalingam
MIMO-Zak-OTFS with Superimposed Spread Pilots
Oct 23, 2025Abstract:In this paper, we consider the problem of spread pilot design and effective channel estimation in multiple-input multiple-output Zak-OTFS (MIMO-Zak-OTFS) with superimposed spread pilots, where data and spread pilot signals are superimposed in the same frame. To achieve good estimation performance in a MIMO setting, the spread pilots at different transmit antennas need to be effectively separated at the receiver. Towards this, we propose a spread pilot design that separates the pilot sequences in the cross-ambiguity domain and enables the estimation of the effective channel taps by a simple read-off operation. To further alleviate the effect of pilot-data interference on performance, we carry out turbo iterations between channel estimation and detection. Simulation results for $2\times 2$ and $3\times 3$ MIMO-Zak-OTFS with Gaussian-sinc pulse shaping filter for vehicular-A channel model show that the proposed pilot design and estimation scheme with three turbo iterations can achieve very good estimation/detection performance.
Zak-OTFS over CP-OFDM
Aug 05, 2025Abstract:Zak-Orthogonal Time Frequency Space (Zak-OTFS) modulation has been shown to achieve significantly better performance compared to the standardized Cyclic-Prefix Orthogonal Frequency Division Multiplexing (CP-OFDM), in high delay/Doppler spread scenarios envisaged in next generation communication systems. Zak-OTFS carriers are quasi-periodic pulses in the delay-Doppler (DD) domain, characterized by two parameters, (i) the pulse period along the delay axis (``delay period") (Doppler period is related to the delay period), and (ii) the pulse shaping filter. An important practical challenge is enabling support for Zak-OTFS modulation in existing CP-OFDM based modems. In this paper we show that Zak-OTFS modulation with pulse shaping constrained to sinc filtering (filter bandwidth equal to the communication bandwidth $B$) followed by time-windowing with a rectangular window of duration $(T + T_{cp})$ ($T$ is the symbol duration and $T_{cp}$ is the CP duration), can be implemented as a low-complexity precoder over standard CP-OFDM. We also show that the Zak-OTFS de-modulator with matched filtering constrained to sinc filtering (filter bandwidth $B$) followed by rectangular time windowing over duration $T$ can be implemented as a low-complexity post-processing of the CP-OFDM de-modulator output. This proposed ``Zak-OTFS over CP-OFDM" architecture enables us to harness the benefits of Zak-OTFS in existing network infrastructure. We also show that the proposed Zak-OTFS over CP-OFDM is a family of modulations, with CP-OFDM being a special case when the delay period takes its minimum possible value equal to the inverse bandwidth, i.e., Zak-OTFS over CP-OFDM with minimum delay period.
Waveform for Next Generation Communication Systems: Comparing Zak-OTFS with OFDM
May 20, 2025

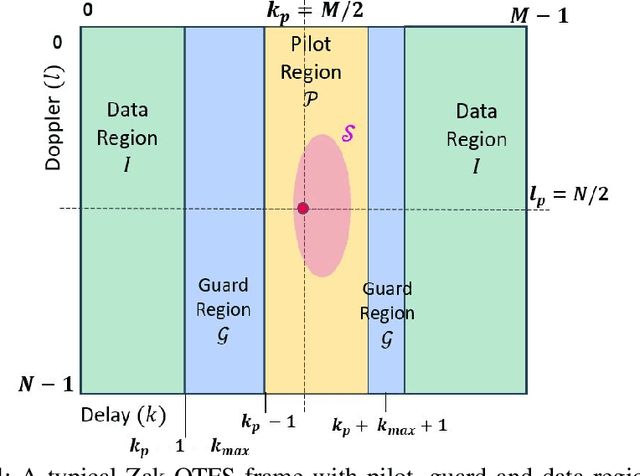
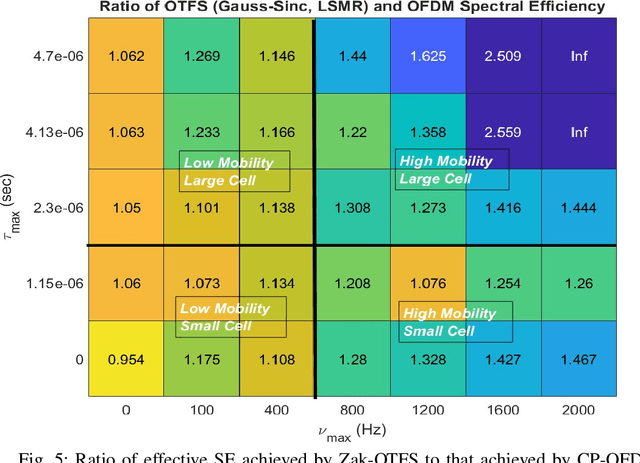
Abstract:Across the world, there is growing interest in new waveforms, Zak-OTFS in particular, and over-the-air implementations are starting to appear. The choice between OFDM and Zak-OTFS is not so much a choice between waveforms as it is an architectural choice between preventing inter-carrier interference (ICI) and embracing ICI. In OFDM, once the Input-Output (I/O) relation is known, equalization is relatively simple, at least when there is no ICI. However, in the presence of ICI the I/O relation is non-predictable and its acquisition is non-trivial. In contrast, equalization is more involved in Zak-OTFS due to inter-symbol-interference (ISI), however the I/O relation is predictable and its acquisition is simple. {Zak-OTFS exhibits superior performance in doubly-spread 6G use cases with high delay/Doppler channel spreads (i.e., high mobility and/or large cells), but architectural choice is governed by the typical use case, today and in the future. What is typical depends to some degree on geography, since large delay spread is a characteristic of large cells which are the rule rather than the exception in many important wireless markets.} This paper provides a comprehensive performance comparison of cyclic prefix OFDM (CP-OFDM) and Zak-OTFS across the full range of 6G propagation environments. The performance results provide insights into the fundamental architectural choice.
Closed-Form Expressions for I/O Relation in Zak-OTFS with Different Delay-Doppler Filters
Apr 26, 2025Abstract:The transceiver operations in the delay-Doppler (DD) domain in Zak-OTFS modulation, including DD domain filtering at the transmitter and receiver, involve twisted convolution operation. The twisted convolution operations give rise to multiple integrals in the end-to-end DD domain input-output (I/O) relation. The I/O relation plays a crucial role in performance evaluation and algorithm development for transceiver implementation. In this paper, we derive discrete DD domain closed-form expressions for the I/O relation and noise covariance in Zak-OTFS. We derive these expressions for sinc and Gaussian pulse shaping DD filters at the transmitter (Tx). On the receiver (Rx) side, three types of DD filters are considered, viz., $(i)$ Rx filter identical to Tx filter (referred to as `identical filtering'), $(ii)$ Rx filter matched to the Tx filter (referred to as `matched filtering'), and $(iii)$ Rx filter matched to both Tx filter and channel response (referred to as `channel matched filtering'). For all the above cases, except for the case of sinc identical filtering, we derive exact I/O relation and noise covariance expressions in closed-form. For the sinc identical filtering case, we derive approximate closed-form expressions which are shown to be accurate. Using the derived closed-form expressions, we evaluate the bit error performance of Zak-OTFS for different Tx/Rx filter configurations. Our results using Vehicular-A (Veh-A) channel model with fractional DDs show that, while matched filtering achieves slightly better or almost same performance as identical filtering, channel matched filtering achieves the best performance among the three.
Zak-OTFS for Identification of Linear Time-Varying Systems
Mar 24, 2025Abstract:Linear time-varying (LTV) systems model radar scenes where each reflector/target applies a delay, Doppler shift and complex amplitude scaling to a transmitted waveform. The receiver processes the received signal using the transmitted signal as a reference. The self-ambiguity function of the transmitted signal captures the cross-correlation of delay and Doppler shifts of the transmitted waveform. It acts as a blur that limits resolution, at the receiver, of the delay and Doppler shifts of targets in close proximity. This paper considers resolution of multiple targets and compares performance of traditional chirp waveforms with the Zak-OTFS waveform. The self-ambiguity function of a chirp is a line in the delay-Doppler domain, whereas the self-ambiguity function of the Zak-OTFS waveform is a lattice. The advantage of lattices over lines is better localization, and we show lattices provide superior noise-free estimation of the range and velocity of multiple targets. When the delay spread of the radar scene is less than the delay period of the Zak-OTFS modulation, and the Doppler spread is less than the Doppler period, we describe how to localize targets by calculating cross-ambiguities in the delay-Doppler domain. We show that the signal processing complexity of our approach is superior to the traditional approach of computing cross-ambiguities in the continuous time / frequency domain.
A Gaussian-Sinc Pulse Shaping Filter for Zak-OTFS
Feb 06, 2025



Abstract:The choice of delay-Doppler domain (DD) pulse shaping filter plays an important role in determining the performance of Zak-OTFS. Sinc filter has good main lobe characteristics (with nulls at information grid points) which is good for equalization/detection, but has high side lobes which are detrimental for input-output (I/O) relation estimation. Whereas, Gaussian filter is highly localized with very low side lobes which is good for I/O relation estimation, but has poor main lobe characteristics which is not good for equalization/detection. In this paper, we propose a new filter, termed as {\em Gaussian-sinc (GS) filter}, which inherits the complementary strengths of both Gaussian and sinc filters. The proposed filter does not incur time or bandwidth expansion. We derive closed-form expressions for the I/O relation and noise covariance of Zak-OTFS with the proposed GS filter. We evaluate the Zak-OTFS performance for different pulse shaping filters with I/O relation estimated using exclusive and embedded pilots. Our results show that the proposed GS filter achieves better bit error rate (BER) performance compared to other filters reported in the literature. For example, with model-free I/O relation estimation using embedded pilot and 8-QAM, the proposed GS filter achieves an SNR gain of about 4 dB at $10^{-2}$ uncoded BER compared to Gaussian and sinc filters, and the SNR gain becomes more than 6 dB at a coded BER of $10^{-4}$ with rate-1/2 coding.
Zak-OTFS with Interleaved Pilots to Extend the Region of Predictable Operation
Aug 18, 2024Abstract:When the delay period of the Zak-OTFS carrier is greater than the delay spread of the channel, and the Doppler period of the carrier is greater than the Doppler spread of the channel, the effective channel filter taps can simply be read off from the response to a single pilot carrier waveform. The input-output (I/O) relation can then be reconstructed for a sampled system that operates under finite duration and bandwidth constraints. We introduce a framework for pilot design in the delay-Doppler (DD) domain which makes it possible to support users with very different delay-Doppler characteristics when it is not possible to choose a single delay and Doppler period to support all users. The method is to interleave single pilots in the DD domain, and to choose the pilot spacing so that the I/O relation can be reconstructed by solving a small linear system of equations.
Zak-OTFS and Turbo Signal Processing for Joint Sensing and Communication
Jun 10, 2024



Abstract:The Zak-OTFS input/output (I/O) relation is predictable and non-fading when the delay and Doppler periods are greater than the effective channel delay and Doppler spreads, a condition which we refer to as the crystallization condition. The filter taps can simply be read off from the response to a single Zak-OTFS pilot pulsone, and the I/O relation can be reconstructed for a sampled system that operates under finite duration and bandwidth constraints. In previous work we had measured BER performance of a baseline system where we used separate Zak-OTFS subframes for sensing and data transmission. In this Letter we demonstrate how to use turbo signal processing to match BER performance of this baseline system when we integrate sensing and communication within the same Zak-OTFS subframe. The turbo decoder alternates between channel sensing using a noise-like waveform (spread pulsone) and recovery of data transmitted using point pulsones.
Zak-OTFS: Pulse Shaping and the Tradeoff between Time/Bandwidth Expansion and Predictability
May 04, 2024Abstract:The Zak-OTFS input/output (I/O) relation is predictable and non-fading when the delay and Doppler periods are greater than the effective channel delay and Doppler spreads, a condition which we refer to as the crystallization condition. When the crystallization condition is satisfied, we describe how to integrate sensing and communication within a single Zak-OTFS subframe by transmitting a pilot in the center of the subframe and surrounding the pilot with a pilot region and guard band to mitigate interference between data symbols and pilot. At the receiver we first read off the effective channel taps within the pilot region, and then use the estimated channel taps to recover the data from the symbols received outside the pilot region. We introduce a framework for filter design in the delay-Doppler (DD) domain where the symplectic Fourier transform connects aliasing in the DD domain (predictability of the I/O relation) with time/bandwidth expansion. The choice of pulse shaping filter determines the fraction of pilot energy that lies outside the pilot region and the degradation in BER performance that results from the interference to data symbols. We demonstrate that Gaussian filters in the DD domain provide significant improvements in BER performance over the sinc and root raised cosine filters considered in previous work. We also demonstrate that, by limiting DD domain aliasing, Gaussian filters extend the region where the crystallization condition is satisfied. The Gaussian filters considered in this paper are a particular case of factorizable pulse shaping filters in the DD domain, and this family of filters may be of independent interest.
Zak-OTFS for Integration of Sensing and Communication
Apr 05, 2024Abstract:The Zak-OTFS input/output (I/O) relation is predictable and non-fading when the delay and Doppler periods are greater than the effective channel delay and Doppler spreads, a condition which we refer to as the crystallization condition. The filter taps can simply be read off from the response to a single Zak-OTFS point (impulse) pulsone waveform, and the I/O relation can be reconstructed for a sampled system that operates under finite duration and bandwidth constraints. Predictability opens up the possibility of a model-free mode of operation. The time-domain realization of a Zak-OTFS point pulsone is a pulse train modulated by a tone, hence the name, pulsone. The Peak-to-Average Power Ratio (PAPR) of a pulsone is about $15$ dB, and we describe a general method for constructing a spread pulsone for which the time-domain realization has a PAPR of about 6dB. We construct the spread pulsone by applying a type of discrete spreading filter to a Zak-OTFS point pulsone. The self-ambiguity function of the point pulsone is supported on the period lattice ${\Lambda}_{p}$, and by applying a discrete chirp filter, we obtain a spread pulsone with a self-ambiguity function that is supported on a rotated lattice ${\Lambda^*}$. We show that if the channel satisfies the crystallization conditions with respect to ${\Lambda^*}$ then the effective DD domain filter taps can simply be read off from the cross-ambiguity between the channel response to the spread pulsone and the transmitted spread pulsone. If, in addition, the channel satisfies the crystallization conditions with respect to the period lattice ${\Lambda}_{p}$, then in an OTFS frame consisting of a spread pilot pulsone and point data pulsones, after cancelling the received signal corresponding to the spread pulsone, we can recover the channel response to any data pulsone.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge