Diffusion Model Based Resource Allocation Strategy in Ultra-Reliable Wireless Networked Control Systems

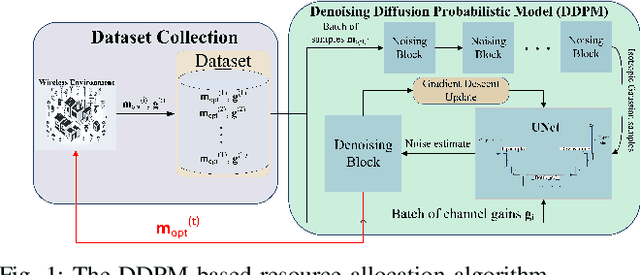
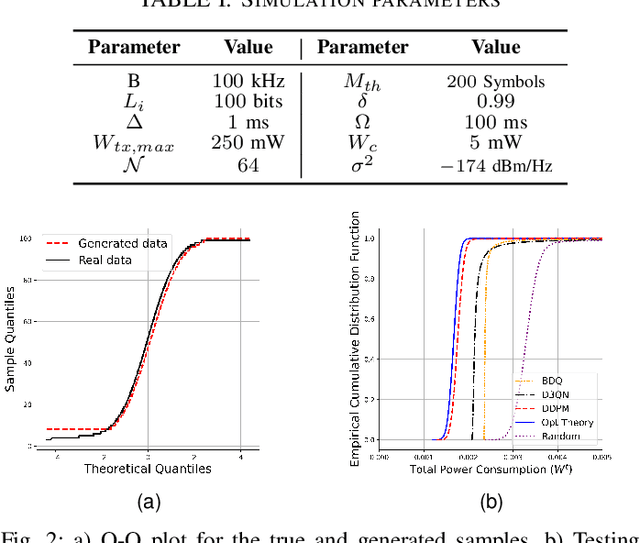
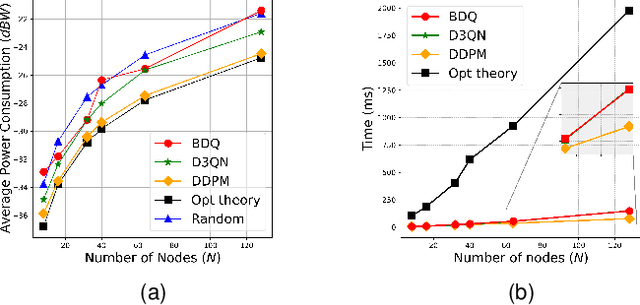
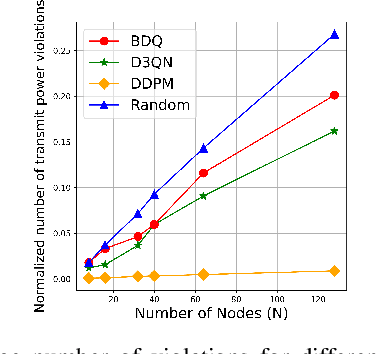
Diffusion models are vastly used in generative AI, leveraging their capability to capture complex data distributions. However, their potential remains largely unexplored in the field of resource allocation in wireless networks. This paper introduces a novel diffusion model-based resource allocation strategy for Wireless Networked Control Systems (WNCSs) with the objective of minimizing total power consumption through the optimization of the sampling period in the control system, and blocklength and packet error probability in the finite blocklength regime of the communication system. The problem is first reduced to the optimization of blocklength only based on the derivation of the optimality conditions. Then, the optimization theory solution collects a dataset of channel gains and corresponding optimal blocklengths. Finally, the Denoising Diffusion Probabilistic Model (DDPM) uses this collected dataset to train the resource allocation algorithm that generates optimal blocklength values conditioned on the channel state information (CSI). Via extensive simulations, the proposed approach is shown to outperform previously proposed Deep Reinforcement Learning (DRL) based approaches with close to optimal performance regarding total power consumption. Moreover, an improvement of up to eighteen-fold in the reduction of critical constraint violations is observed, further underscoring the accuracy of the solution.

Optimization Theory Based Deep Reinforcement Learning for Resource Allocation in Ultra-Reliable Wireless Networked Control Systems

The design of Wireless Networked Control System (WNCS) requires addressing critical interactions between control and communication systems with minimal complexity and communication overhead while providing ultra-high reliability. This paper introduces a novel optimization theory based deep reinforcement learning (DRL) framework for the joint design of controller and communication systems. The objective of minimum power consumption is targeted while satisfying the schedulability and rate constraints of the communication system in the finite blocklength regime and stability constraint of the control system. Decision variables include the sampling period in the control system, and blocklength and packet error probability in the communication system. The proposed framework contains two stages: optimization theory and DRL. In the optimization theory stage, following the formulation of the joint optimization problem, optimality conditions are derived to find the mathematical relations between the optimal values of the decision variables. These relations allow the decomposition of the problem into multiple building blocks. In the DRL stage, the blocks that are simplified but not tractable are replaced by DRL. Via extensive simulations, the proposed optimization theory based DRL approach is demonstrated to outperform the optimization theory and pure DRL based approaches, with close to optimal performance and much lower complexity.