Context-Aware Automated Passenger Counting Data Denoising

A reliable and accurate knowledge of the ridership in public transportation networks is crucial for public transport operators and public authorities to be aware of their network's use and optimize transport offering. Several techniques to estimate ridership exist nowadays, some of them in an automated manner. Among them, Automatic Passenger Counting (APC) systems detect passengers entering and leaving the vehicle at each station of its course. However, data resulting from these systems are often noisy or even biased, resulting in under or overestimation of onboard occupancy. In this work, we propose a denoising algorithm for APC data to improve their robustness and ease their analyzes. The proposed approach consists in a constrained integer linear optimization, taking advantage of ticketing data and historical ridership data to further constrain and guide the optimization. The performances are assessed and compared to other denoising methods on several public transportation networks in France, to manual counts available on one of these networks, and on simulated data.

Quantized Variational Inference

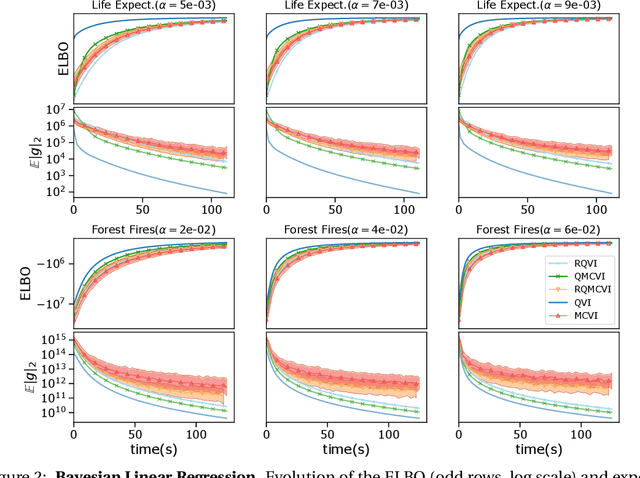
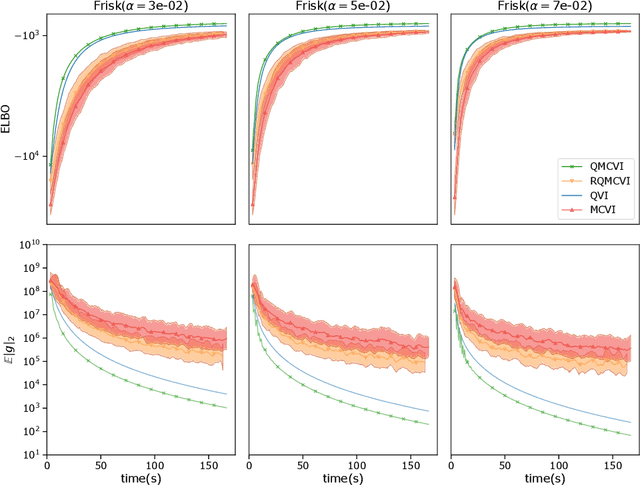
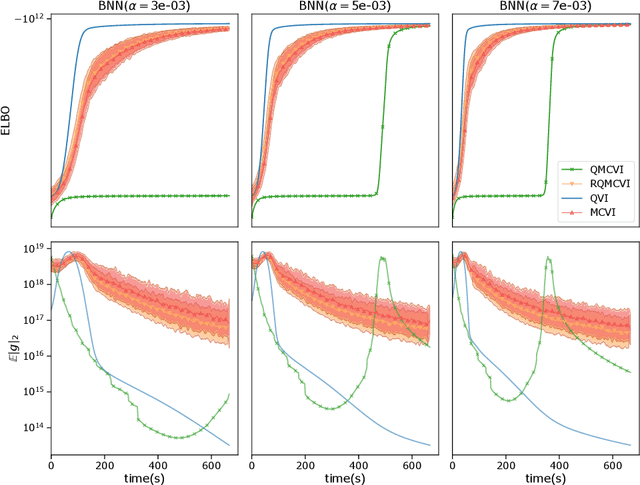
We present Quantized Variational Inference, a new algorithm for Evidence Lower Bound maximization. We show how Optimal Voronoi Tesselation produces variance free gradients for ELBO optimization at the cost of introducing asymptotically decaying bias. Subsequently, we propose a Richardson extrapolation type method to improve the asymptotic bound. We show that using the Quantized Variational Inference framework leads to fast convergence for both score function and the reparametrized gradient estimator at a comparable computational cost. Finally, we propose several experiments to assess the performance of our method and its limitations.