Alphin J. Thottupattu
A method for large diffeomorphic registration via broken geodesics
Jan 03, 2021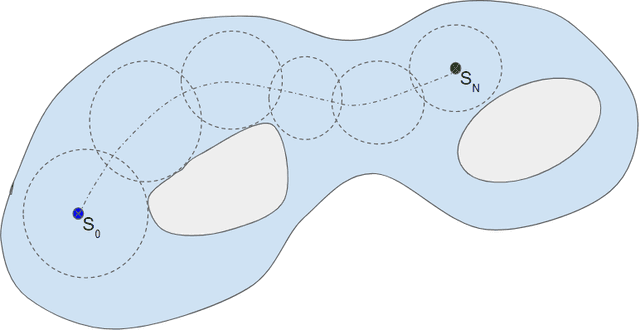



Abstract:Anatomical variabilities seen in longitudinal data or inter-subject data is usually described by the underlying deformation, captured by non-rigid registration of these images. Stationary Velocity Field (SVF) based non-rigid registration algorithms are widely used for registration. SVF based methods form a metric-free framework which captures a finite dimensional submanifold of deformations embedded in the infinite dimensional smooth manifold of diffeomorphisms. However, these methods cover only a limited degree of deformations. In this paper, we address this limitation and define an approximate metric space for the manifold of diffeomorphisms $\mathcal{G}$. We propose a method to break down the large deformation into finite compositions of small deformations. This results in a broken geodesic path on $\mathcal{G}$ and its length now forms an approximate registration metric. We illustrate the method using a simple, intensity-based, log-demon implementation. Validation results of the proposed method show that it can capture large and complex deformations while producing qualitatively better results than the state-of-the-art methods. The results also demonstrate that the proposed registration metric is a good indicator of the degree of deformation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge