Alla Kammerdiner
Multidimensional Assignment Problem for multipartite entity resolution
Dec 06, 2021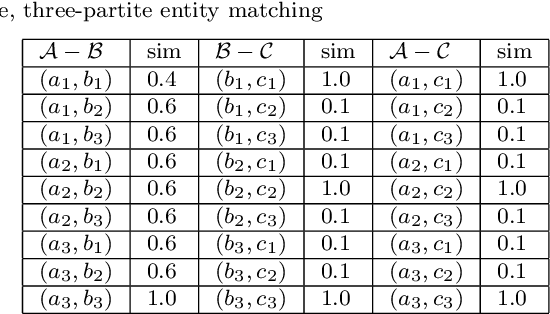
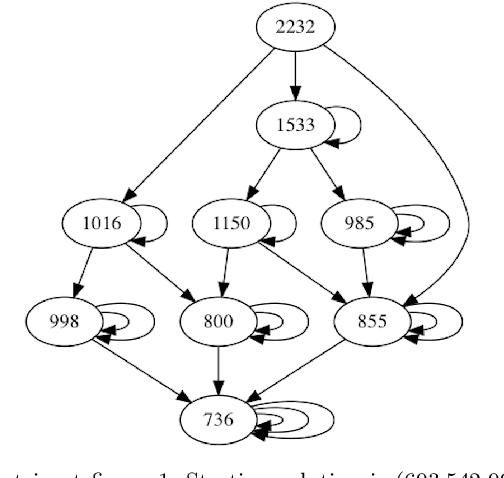
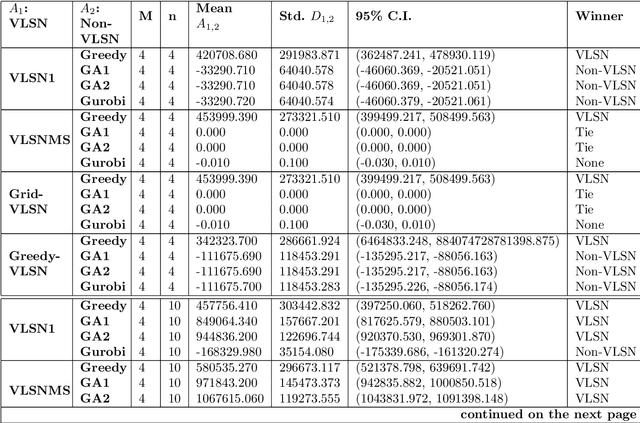
Abstract:Multipartite entity resolution aims at integrating records from multiple datasets into one entity. We derive a mathematical formulation for a general class of record linkage problems in multipartite entity resolution across many datasets as a combinatorial optimization problem known as the multidimensional assignment problem. As a motivation for our approach, we illustrate the advantage of multipartite entity resolution over sequential bipartite matching. Because the optimization problem is NP-hard, we apply two heuristic procedures, a Greedy algorithm and very large scale neighborhood search, to solve the assignment problem and find the most likely matching of records from multiple datasets into a single entity. We evaluate and compare the performance of these algorithms and their modifications on synthetically generated data. We perform computational experiments to compare performance of recent heuristic, the very large-scale neighborhood search, with a Greedy algorithm, another heuristic for the MAP, as well as with two versions of genetic algorithm, a general metaheuristic. Importantly, we perform experiments to compare two alternative methods of re-starting the search for the former heuristic, specifically a random-sampling multi-start and a deterministic design-based multi-start. We find evidence that design-based multi-start can be more efficient as the size of databases grow large. In addition, we show that very large scale search, especially its multi-start version, outperforms simple Greedy heuristic. Hybridization of Greedy search with very large scale neighborhood search improves the performance. Using multi-start with as few as three additional runs of very large scale search offers some improvement in the performance of the very large scale search procedure. Last, we propose an approach to evaluating complexity of the very large-scale neighborhood search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge