A variational Bayes approach to debiased inference for low-dimensional parameters in high-dimensional linear regression

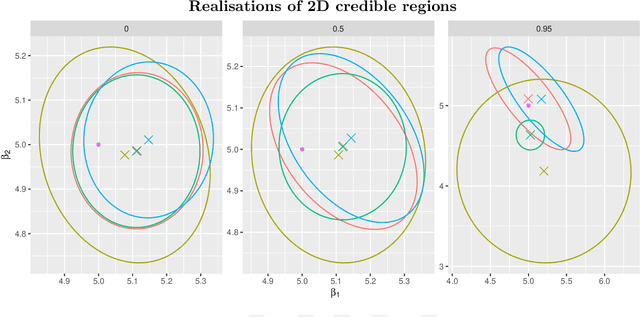
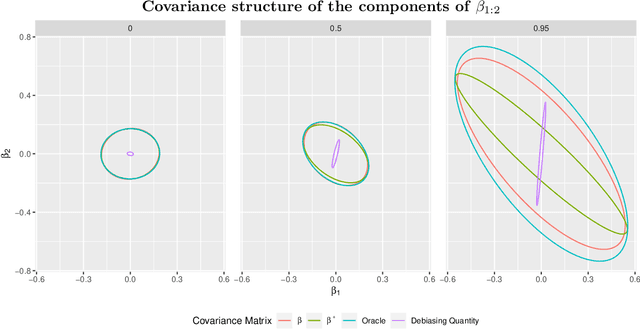
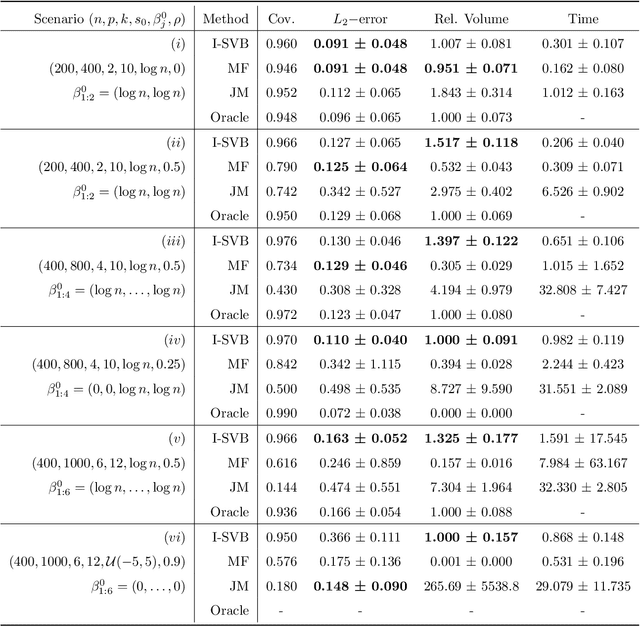
We propose a scalable variational Bayes method for statistical inference for a single or low-dimensional subset of the coordinates of a high-dimensional parameter in sparse linear regression. Our approach relies on assigning a mean-field approximation to the nuisance coordinates and carefully modelling the conditional distribution of the target given the nuisance. This requires only a preprocessing step and preserves the computational advantages of mean-field variational Bayes, while ensuring accurate and reliable inference for the target parameter, including for uncertainty quantification. We investigate the numerical performance of our algorithm, showing that it performs competitively with existing methods. We further establish accompanying theoretical guarantees for estimation and uncertainty quantification in the form of a Bernstein--von Mises theorem.

Semiparametric inference using fractional posteriors

We establish a general Bernstein--von Mises theorem for approximately linear semiparametric functionals of fractional posterior distributions based on nonparametric priors. This is illustrated in a number of nonparametric settings and for different classes of prior distributions, including Gaussian process priors. We show that fractional posterior credible sets can provide reliable semiparametric uncertainty quantification, but have inflated size. To remedy this, we further propose a \textit{shifted-and-rescaled} fractional posterior set that is an efficient confidence set having optimal size under regularity conditions. As part of our proofs, we also refine existing contraction rate results for fractional posteriors by sharpening the dependence of the rate on the fractional exponent.