On-line Parameter Estimation of the Polarization Curve of a Fuel Cell with Guaranteed Convergence Properties: Theoretical and Experimental Results

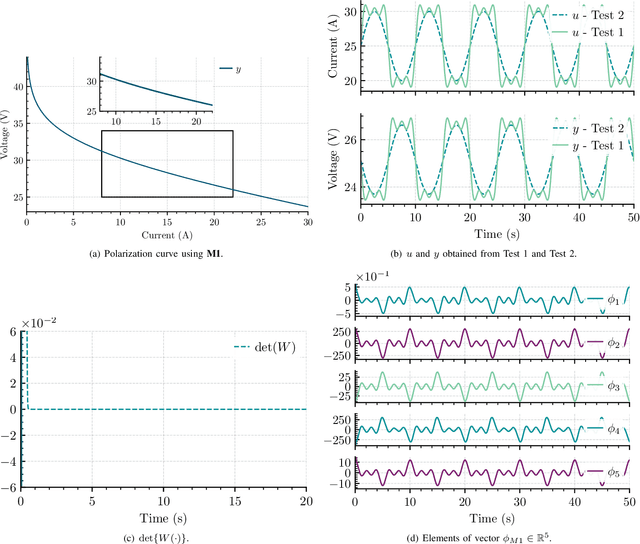
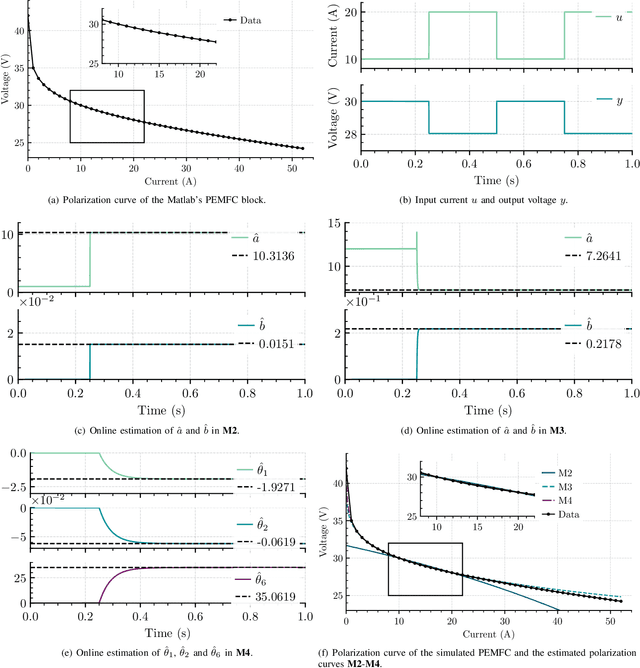
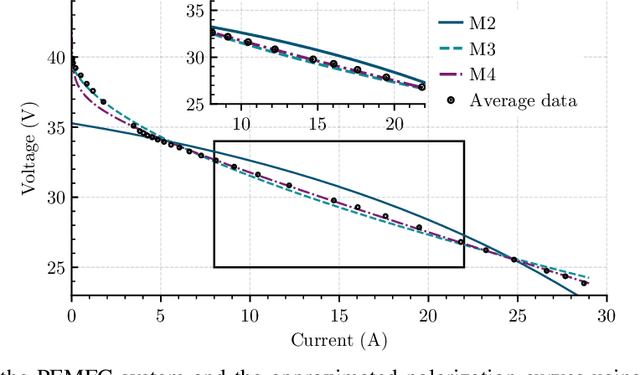
In this paper, we address the problem of online parameter estimation of a Proton Exchange Membrane Fuel Cell (PEMFC) polarization curve, that is the static relation between the voltage and the current of the PEMFC. The task of designing this estimator -- even off-line -- is complicated by the fact that the uncertain parameters enter the curve in a highly nonlinear fashion, namely in the form of nonseparable nonlinearities. We consider several scenarios for the model of the polarization curve, starting from the standard full model and including several popular simplifications to this complicated mathematical function. In all cases, we derive separable regression equations -- either linearly or nonlinearly parameterized -- which are instrumental for the implementation of the parameter estimators. We concentrate our attention on on-line estimation schemes for which, under suitable excitation conditions, global parameter convergence is ensured. Due to these global convergence properties, the estimators are robust to unavoidable additive noise and structural uncertainty. Moreover, their on-line nature endows the schemes with the ability to track (slow) parameter variations, that occur during the operation of the PEMFC. These two features -- unavailable in time-consuming off-line data-fitting procedures -- make the proposed estimators helpful for on-line time-saving characterization of a given PEMFC, and the implementation of fault-detection procedures and model-based adaptive control strategies. Simulation and experimental results that validate the theoretical claims are presented.

An Adaptive Observer for Uncertain Linear Time-Varying Systems with Unknown Additive Perturbations

In this paper we are interested in the problem of adaptive state observation of linear time-varying (LTV) systems where the system and the input matrices depend on unknown time-varying parameters. It is assumed that these parameters satisfy some known LTV dynamics, but with unknown initial conditions. Moreover, the state equation is perturbed by an additive signal generated from an exosystem with uncertain constant parameters. Our main contribution is to propose a globally convergent state observer that requires only a weak excitation assumption on the system.