Alexander W. Churchill
Learning to Generate Genotypes with Neural Networks
Apr 14, 2016

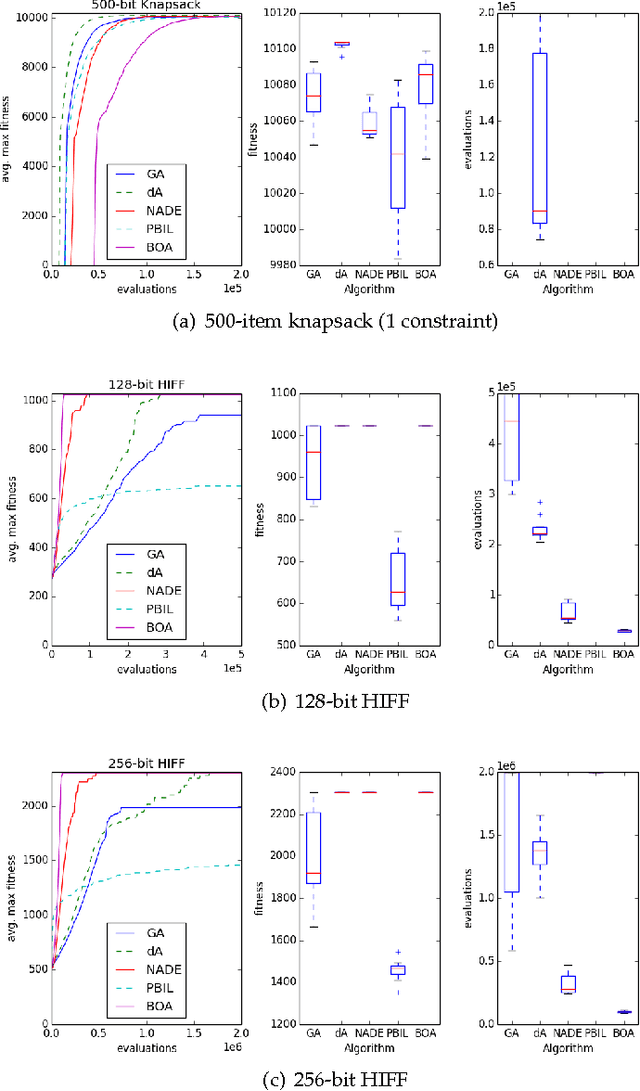

Abstract:Neural networks and evolutionary computation have a rich intertwined history. They most commonly appear together when an evolutionary algorithm optimises the parameters and topology of a neural network for reinforcement learning problems, or when a neural network is applied as a surrogate fitness function to aid the evolutionary optimisation of expensive fitness functions. In this paper we take a different approach, asking the question of whether a neural network can be used to provide a mutation distribution for an evolutionary algorithm, and what advantages this approach may offer? Two modern neural network models are investigated, a Denoising Autoencoder modified to produce stochastic outputs and the Neural Autoregressive Distribution Estimator. Results show that the neural network approach to learning genotypes is able to solve many difficult discrete problems, such as MaxSat and HIFF, and regularly outperforms other evolutionary techniques.
A Denoising Autoencoder that Guides Stochastic Search
Apr 06, 2014

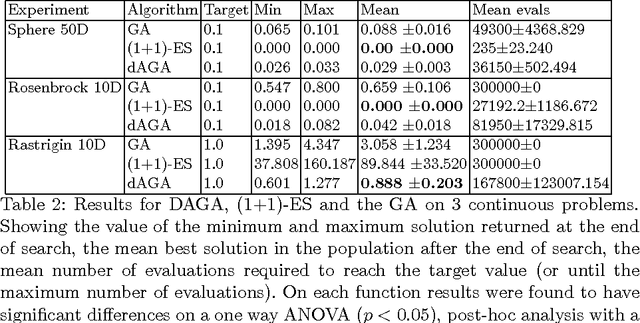

Abstract:An algorithm is described that adaptively learns a non-linear mutation distribution. It works by training a denoising autoencoder (DA) online at each generation of a genetic algorithm to reconstruct a slowly decaying memory of the best genotypes so far. A compressed hidden layer forces the autoencoder to learn hidden features in the training set that can be used to accelerate search on novel problems with similar structure. Its output neurons define a probability distribution that we sample from to produce offspring solutions. The algorithm outperforms a canonical genetic algorithm on several combinatorial optimisation problems, e.g. multidimensional 0/1 knapsack problem, MAXSAT, HIFF, and on parameter optimisation problems, e.g. Rastrigin and Rosenbrock functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge