Continuous Time-Delay Estimation From Sampled Measurements

An algorithm for continuous time-delay estimation from sampled output data and known input of finite energy is presented. The continuous time-delay modeling allows for the estimation of subsample delays. The proposed estimation algorithm consists of two steps. First, the continuous Laguerre spectrum of the output signal is estimated from discrete-time (sampled) noisy measurements. Second, an estimate of the delay value is obtained in Laguerre domain given a continuous-time description of the input. The second step of the algorithm is shown to be intrinsically biased, the bias sources are established, and the bias itself is modeled. The proposed delay estimation approach is compared in a Monte-Carlo simulation with state-of-the-art methods implemented in time, frequency, and Laguerre domain demonstrating comparable or higher accuracy for the considered case.

Noise reduction in Laguerre-domain discrete delay estimation

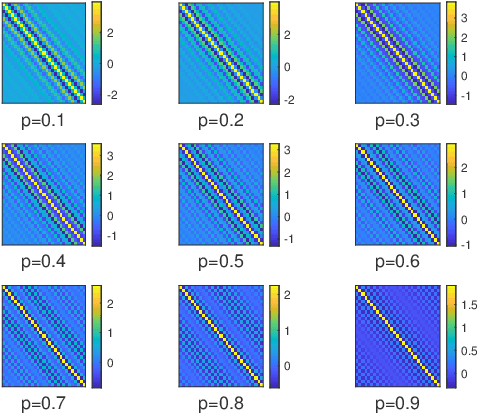
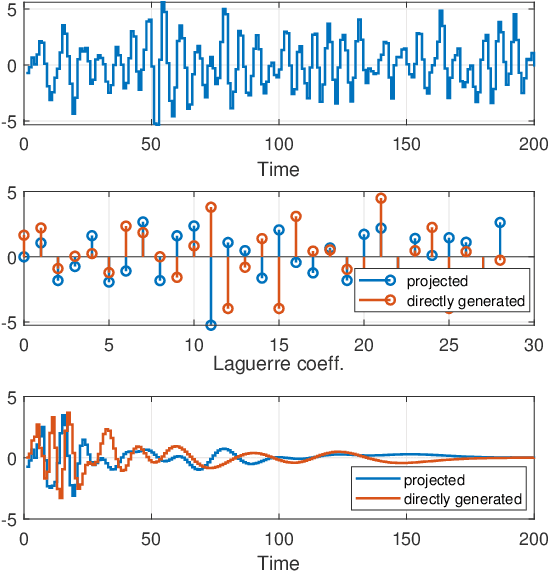
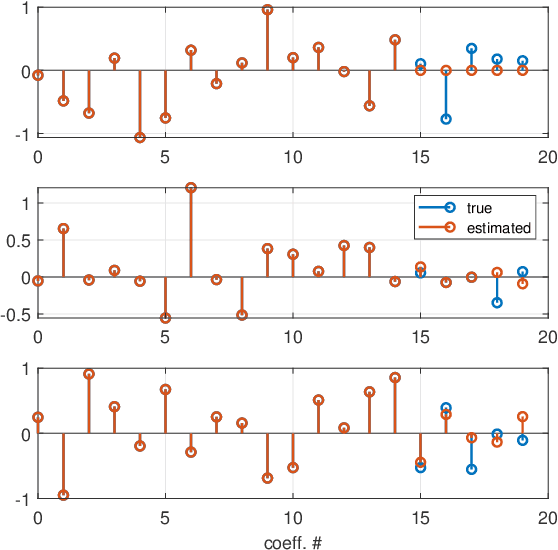
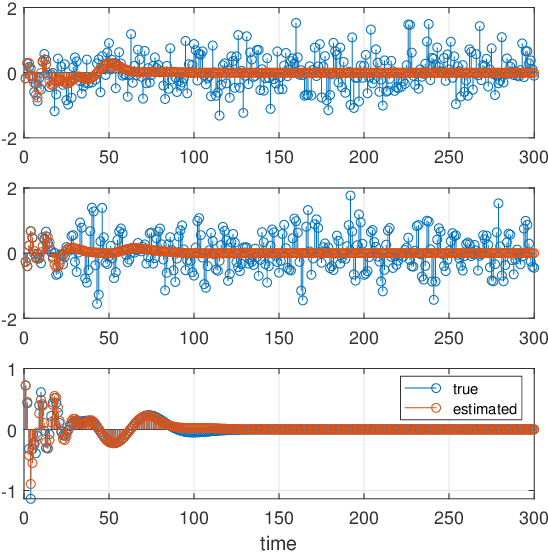
This paper introduces a stochastic framework for a recently proposed discrete-time delay estimation method in Laguerre-domain, i.e. with the delay block input and output signals being represented by the corresponding Laguerre series. A novel Laguerre domain disturbance model is devised, which allows the involved signals to be square-summable sequences and is suitable in a number of important applications. The relation to two commonly used time-domain disturbance models is clarified. Furthermore, by forming the input signal in a certain way, the signal shape of an additive output disturbance can be estimated and utilized for noise reduction. It is demonstrated that a significant improvement in the delay estimation error is achieved when the noise sequence is correlated. The noise reduction approach is applicable to other Laguerre-domain problems than pure delay estimation.