Continuous Time-Delay Estimation From Sampled Measurements

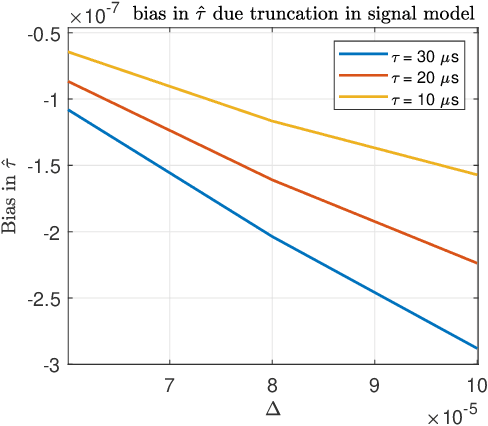
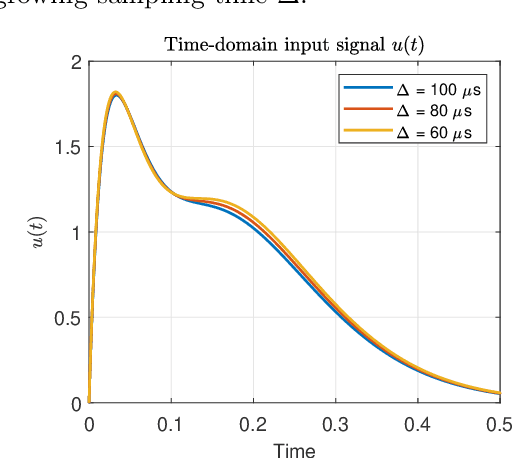
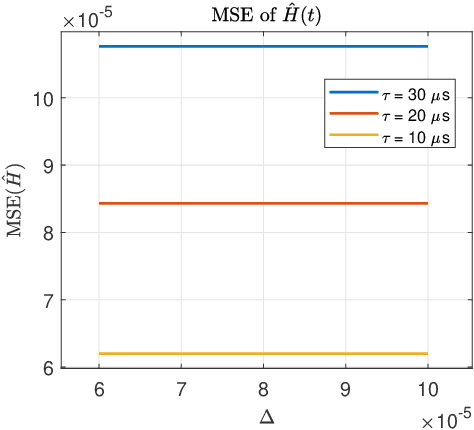
An algorithm for continuous time-delay estimation from sampled output data and known input of finite energy is presented. The continuous time-delay modeling allows for the estimation of subsample delays. The proposed estimation algorithm consists of two steps. First, the continuous Laguerre spectrum of the output signal is estimated from discrete-time (sampled) noisy measurements. Second, an estimate of the delay value is obtained in Laguerre domain given a continuous-time description of the input. The second step of the algorithm is shown to be intrinsically biased, the bias sources are established, and the bias itself is modeled. The proposed delay estimation approach is compared in a Monte-Carlo simulation with state-of-the-art methods implemented in time, frequency, and Laguerre domain demonstrating comparable or higher accuracy for the considered case.