Generative Modelling of Stochastic Rotating Shallow Water Noise

In recent work, the authors have developed a generic methodology for calibrating the noise in fluid dynamics stochastic partial differential equations where the stochasticity was introduced to parametrize subgrid-scale processes. The stochastic parameterization of sub-grid scale processes is required in the estimation of uncertainty in weather and climate predictions, to represent systematic model errors arising from subgrid-scale fluctuations. The previous methodology used a principal component analysis (PCA) technique based on the ansatz that the increments of the stochastic parametrization are normally distributed. In this paper, the PCA technique is replaced by a generative model technique. This enables us to avoid imposing additional constraints on the increments. The methodology is tested on a stochastic rotating shallow water model with the elevation variable of the model used as input data. The numerical simulations show that the noise is indeed non-Gaussian. The generative modelling technology gives good RMSE, CRPS score and forecast rank histogram results.

Deep Learning for the Benes Filter

The Benes filter is a well-known continuous-time stochastic filtering model in one dimension that has the advantage of being explicitly solvable. From an evolution equation point of view, the Benes filter is also the solution of the filtering equations given a particular set of coefficient functions. In general, the filtering stochastic partial differential equations (SPDE) arise as the evolution equations for the conditional distribution of an underlying signal given partial, and possibly noisy, observations. Their numerical approximation presents a central issue for theoreticians and practitioners alike, who are actively seeking accurate and fast methods, especially for such high-dimensional settings as numerical weather prediction, for example. In this paper we present a brief study of a new numerical method based on the mesh-free neural network representation of the density of the solution of the Benes model achieved by deep learning. Based on the classical SPDE splitting method, our algorithm includes a recursive normalisation procedure to recover the normalised conditional distribution of the signal process. Within the analytically tractable setting of the Benes filter, we discuss the role of nonlinearity in the filtering model equations for the choice of the domain of the neural network. Further we present the first study of the neural network method with an adaptive domain for the Benes model.

An application of the splitting-up method for the computation of a neural network representation for the solution for the filtering equations

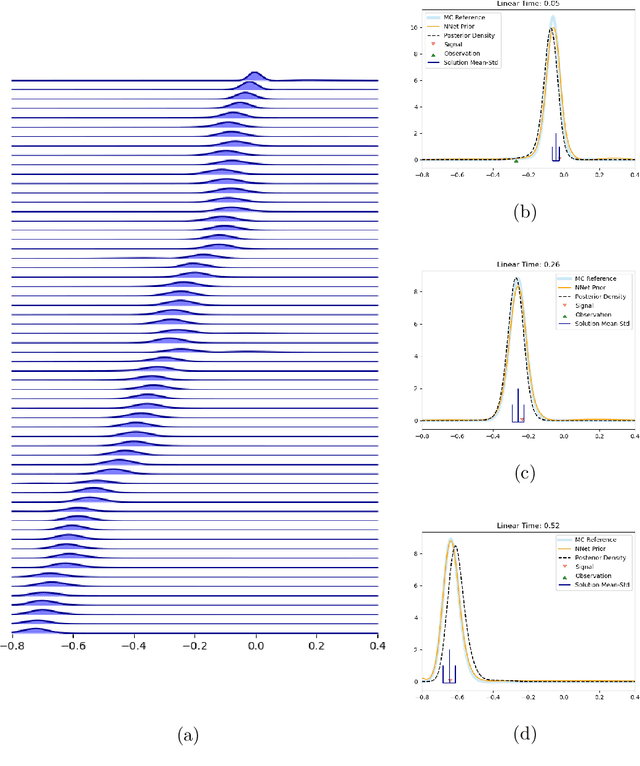
The filtering equations govern the evolution of the conditional distribution of a signal process given partial, and possibly noisy, observations arriving sequentially in time. Their numerical approximation plays a central role in many real-life applications, including numerical weather prediction, finance and engineering. One of the classical approaches to approximate the solution of the filtering equations is to use a PDE inspired method, called the splitting-up method, initiated by Gyongy, Krylov, LeGland, among other contributors. This method, and other PDE based approaches, have particular applicability for solving low-dimensional problems. In this work we combine this method with a neural network representation. The new methodology is used to produce an approximation of the unnormalised conditional distribution of the signal process. We further develop a recursive normalisation procedure to recover the normalised conditional distribution of the signal process. The new scheme can be iterated over multiple time steps whilst keeping its asymptotic unbiasedness property intact. We test the neural network approximations with numerical approximation results for the Kalman and Benes filter.