ForeCite: Adapting Pre-Trained Language Models to Predict Future Citation Rates of Academic Papers

Predicting the future citation rates of academic papers is an important step toward the automation of research evaluation and the acceleration of scientific progress. We present $\textbf{ForeCite}$, a simple but powerful framework to append pre-trained causal language models with a linear head for average monthly citation rate prediction. Adapting transformers for regression tasks, ForeCite achieves a test correlation of $\rho = 0.826$ on a curated dataset of 900K+ biomedical papers published between 2000 and 2024, a 27-point improvement over the previous state-of-the-art. Comprehensive scaling-law analysis reveals consistent gains across model sizes and data volumes, while temporal holdout experiments confirm practical robustness. Gradient-based saliency heatmaps suggest a potentially undue reliance on titles and abstract texts. These results establish a new state-of-the-art in forecasting the long-term influence of academic research and lay the groundwork for the automated, high-fidelity evaluation of scientific contributions.

Mapping Galaxy Images Across Ultraviolet, Visible and Infrared Bands Using Generative Deep Learning

We demonstrate that generative deep learning can translate galaxy observations across ultraviolet, visible, and infrared photometric bands. Leveraging mock observations from the Illustris simulations, we develop and validate a supervised image-to-image model capable of performing both band interpolation and extrapolation. The resulting trained models exhibit high fidelity in generating outputs, as verified by both general image comparison metrics (MAE, SSIM, PSNR) and specialized astronomical metrics (GINI coefficient, M20). Moreover, we show that our model can be used to predict real-world observations, using data from the DECaLS survey as a case study. These findings highlight the potential of generative learning to augment astronomical datasets, enabling efficient exploration of multi-band information in regions where observations are incomplete. This work opens new pathways for optimizing mission planning, guiding high-resolution follow-ups, and enhancing our understanding of galaxy morphology and evolution.

PinnDE: Physics-Informed Neural Networks for Solving Differential Equations

In recent years the study of deep learning for solving differential equations has grown substantially. The use of physics-informed neural networks (PINNs) and deep operator networks (DeepONets) have emerged as two of the most useful approaches in approximating differential equation solutions using machine learning. Here, we propose PinnDE, an open-source python library for solving differential equations with both PINNs and DeepONets. We give a brief review of both PINNs and DeepONets, introduce PinnDE along with the structure and usage of the package, and present worked examples to show PinnDE's effectiveness in approximating solutions with both PINNs and DeepONets.

Exactly conservative physics-informed neural networks and deep operator networks for dynamical systems

We introduce a method for training exactly conservative physics-informed neural networks and physics-informed deep operator networks for dynamical systems. The method employs a projection-based technique that maps a candidate solution learned by the neural network solver for any given dynamical system possessing at least one first integral onto an invariant manifold. We illustrate that exactly conservative physics-informed neural network solvers and physics-informed deep operator networks for dynamical systems vastly outperform their non-conservative counterparts for several real-world problems from the mathematical sciences.

Improving physics-informed DeepONets with hard constraints

Current physics-informed (standard or operator) neural networks still rely on accurately learning the initial conditions of the system they are solving. In contrast, standard numerical methods evolve such initial conditions without needing to learn these. In this study, we propose to improve current physics-informed deep learning strategies such that initial conditions do not need to be learned and are represented exactly in the predicted solution. Moreover, this method guarantees that when a DeepONet is applied multiple times to time step a solution, the resulting function is continuous.

Towards replacing precipitation ensemble predictions systems using machine learning

Precipitation forecasts are less accurate compared to other meteorological fields because several key processes affecting precipitation distribution and intensity occur below the resolved scale of global weather prediction models. This requires to use higher resolution simulations. To generate an uncertainty prediction associated with the forecast, ensembles of simulations are run simultaneously. However, the computational cost is a limiting factor here. Thus, instead of generating an ensemble system from simulations there is a trend of using neural networks. Unfortunately the data for high resolution ensemble runs is not available. We propose a new approach to generating ensemble weather predictions for high-resolution precipitation without requiring high-resolution training data. The method uses generative adversarial networks to learn the complex patterns of precipitation and produce diverse and realistic precipitation fields, allowing to generate realistic precipitation ensemble members using only the available control forecast. We demonstrate the feasibility of generating realistic precipitation ensemble members on unseen higher resolutions. We use evaluation metrics such as RMSE, CRPS, rank histogram and ROC curves to demonstrate that our generated ensemble is almost identical to the ECMWF IFS ensemble.

M-ENIAC: A machine learning recreation of the first successful numerical weather forecasts

In 1950 the first successful numerical weather forecast was obtained by solving the barotropic vorticity equation using the Electronic Numerical Integrator and Computer (ENIAC), which marked the beginning of the age of numerical weather prediction. Here, we ask the question of how these numerical forecasts would have turned out, if machine learning based solvers had been used instead of standard numerical discretizations. Specifically, we recreate these numerical forecasts using physics-informed neural networks. We show that physics-informed neural networks provide an easier and more accurate methodology for solving meteorological equations on the sphere, as compared to the ENIAC solver.

Improving physics-informed neural networks with meta-learned optimization

We show that the error achievable using physics-informed neural networks for solving systems of differential equations can be substantially reduced when these networks are trained using meta-learned optimization methods rather than to using fixed, hand-crafted optimizers as traditionally done. We choose a learnable optimization method based on a shallow multi-layer perceptron that is meta-trained for specific classes of differential equations. We illustrate meta-trained optimizers for several equations of practical relevance in mathematical physics, including the linear advection equation, Poisson's equation, the Korteweg--de Vries equation and Burgers' equation. We also illustrate that meta-learned optimizers exhibit transfer learning abilities, in that a meta-trained optimizer on one differential equation can also be successfully deployed on another differential equation.

Model-free machine learning of conservation laws from data

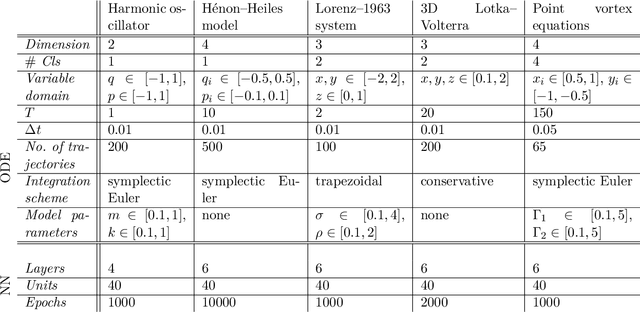
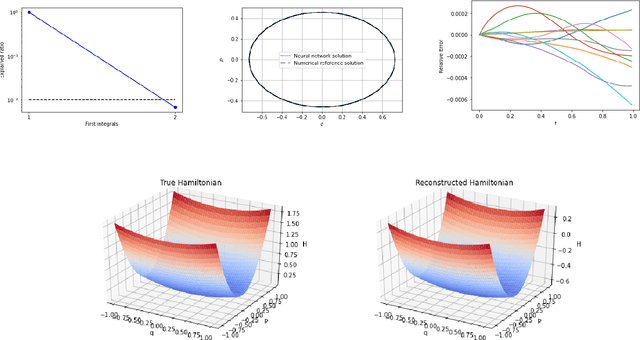
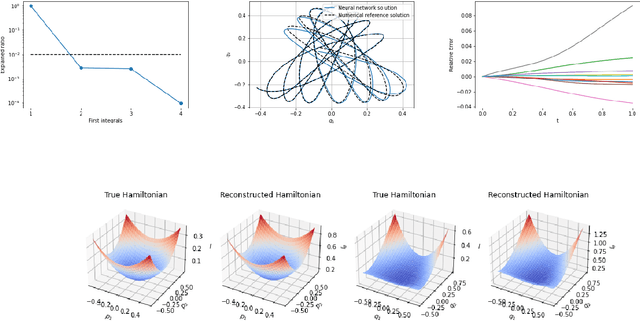
We present a machine learning based method for learning first integrals of systems of ordinary differential equations from given trajectory data. The method is model-free in that it does not require explicit knowledge of the underlying system of differential equations that generated the trajectories. As a by-product, once the first integrals have been learned, also the system of differential equations will be known. We illustrate our method by considering several classical problems from the mathematical sciences.

Improving trajectory calculations using deep learning inspired single image superresolution

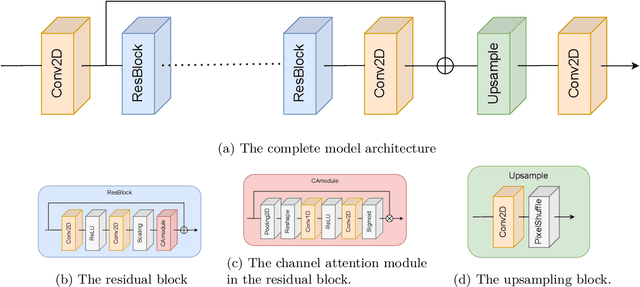
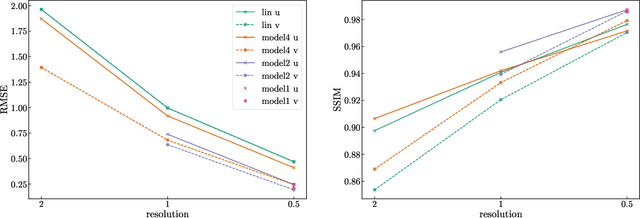
Lagrangian trajectory or particle dispersion models as well as semi-Lagrangian advection schemes require meteorological data such as wind, temperature and geopotential at the exact spatio-temporal locations of the particles that move independently from a regular grid. Traditionally, this high-resolution data has been obtained by interpolating the meteorological parameters from the gridded data of a meteorological model or reanalysis, e.g. using linear interpolation in space and time. However, interpolation errors are a large source of error for these models. Reducing them requires meteorological input fields with high space and time resolution, which may not always be available and can cause severe data storage and transfer problems. Here, we interpret this problem as a single image superresolution task. We interpret meteorological fields available at their native resolution as low-resolution images and train deep neural networks to up-scale them to higher resolution, thereby providing more accurate data for Lagrangian models. We train various versions of the state-of-the-art Enhanced Deep Residual Networks for Superresolution on low-resolution ERA5 reanalysis data with the goal to up-scale these data to arbitrary spatial resolution. We show that the resulting up-scaled wind fields have root-mean-squared errors half the size of the winds obtained with linear spatial interpolation at acceptable computational inference costs. In a test setup using the Lagrangian particle dispersion model FLEXPART and reduced-resolution wind fields, we demonstrate that absolute horizontal transport deviations of calculated trajectories from "ground-truth" trajectories calculated with undegraded 0.5{\deg} winds are reduced by at least 49.5% (21.8%) after 48 hours relative to trajectories using linear interpolation of the wind data when training on 2{\deg} to 1{\deg} (4{\deg} to 2{\deg}) resolution data.