Alejandro J. Garcia
A Comparative Study of Some Central Notions of ASPIC+ and DeLP
Sep 11, 2019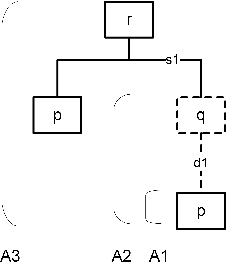
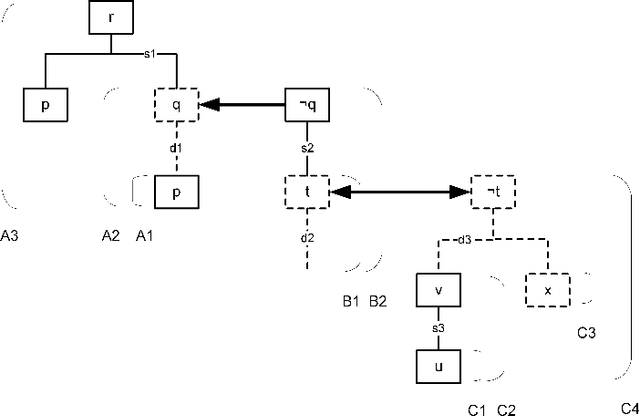
Abstract:This paper formally compares some central notions from two well-known formalisms for rule-based argumentation, DeLP and ASPIC+. The comparisons especially focus on intuitive adequacy and inter-translatability, consistency, and closure properties. As for differences in the definitions of arguments and attack, it turns out that DeLP's definitions are intuitively appealing but that they may not fully comply with Caminada and Amgoud's rationality postulates of strict closure and indirect consistency. For some special cases, the DeLP definitions are shown to fare better than ASPIC+. Next, it is argued that there are reasons to consider a variant of DeLP with grounded semantics, since in some examples its current notion of warrant arguably has counterintuitive consequences and may lead to sets of warranted arguments that are not admissible. Finally, under some minimality and consistency assumptions on ASPIC+ arguments, a one-to-many correspondence between ASPIC+ arguments and DeLP arguments is identified in such a way that if the DeLP warranting procedure is changed to grounded semantics, then DeLP notion of warrant and ASPIC+'s notion of justification are equivalent. This result is proven for three alternative definitions of attack.
An approach to Decision Making based on Dynamic Argumentation Systems
Mar 05, 2019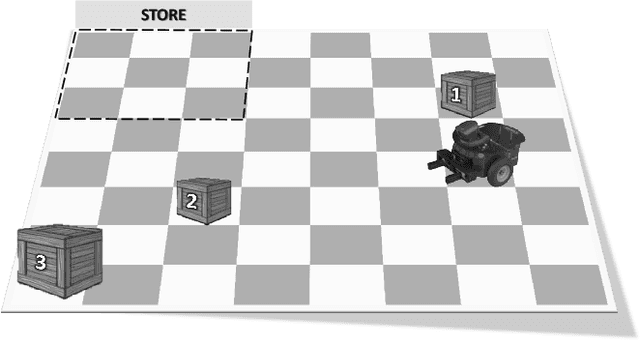

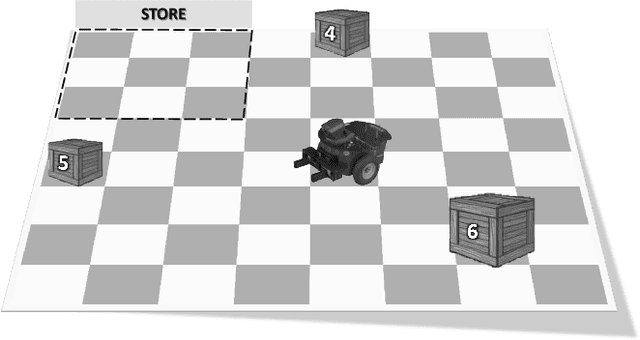
Abstract:In this paper, we introduce a formalism for single-agent decision making that is based on Dynamic Argumentation Frameworks. The formalism can be used to justify a choice, which is based on the current situation the agent is involved. Taking advantage of the inference mechanism of the argumentation formalism, it is possible to consider preference relations and conflicts among the available alternatives for that reasoning. With this formalization, given a particular set of evidence, the justified conclusions supported by warranted arguments will be used by the agent's decision rules to determine which alternatives will be selected. We also present an algorithm that implements a choice function based on our formalization. Finally, we complete our presentation by introducing formal results that relate the proposed framework with approaches of classical decision theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge