Online Allocation and Pricing: Constant Regret via Bellman Inequalities

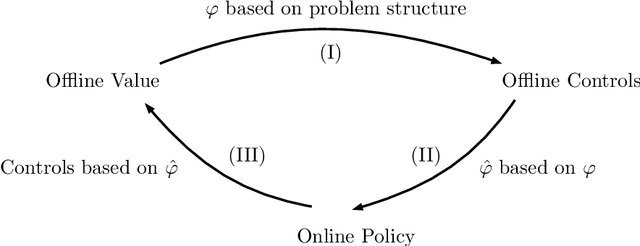
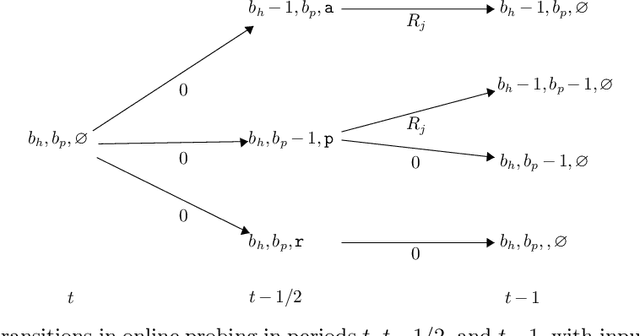
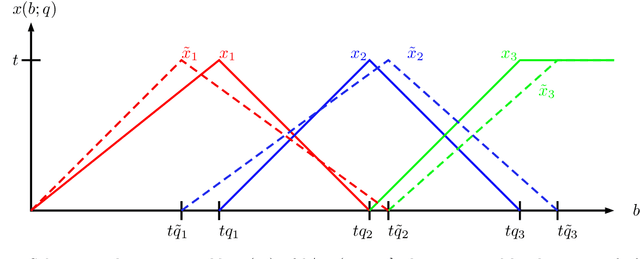
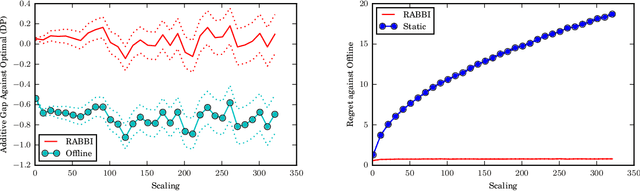
We develop a framework for designing tractable heuristics for Markov Decision Processes (MDP), and use it to obtain constant regret policies for a variety of online allocation problems, including online packing, budget-constrained probing, dynamic pricing, and online contextual bandits with knapsacks. Our approach is based on adaptively constructing a benchmark for the value function, which we then use to select our actions. The centerpiece of our framework are the Bellman Inequalities, which allow us to create benchmarks which both have access to future information, and also, can violate the one-step optimality equations (i.e., Bellman equations). The flexibility of balancing these allows us to get policies which are both tractable and have strong performance guarantees -- in particular, our constant-regret policies only require solving an LP for selecting each action.

The Bayesian Prophet: A Low-Regret Framework for Online Decision Making

Motivated by the success of using black-box predictive algorithms as subroutines for online decision-making, we develop a new framework for designing online policies given access to an oracle providing statistical information about an offline benchmark. Having access to such prediction oracles enables simple and natural Bayesian selection policies, and raises the question as to how these policies perform in different settings. Our work makes two important contributions towards tackling this question: First, we develop a general technique we call *compensated coupling* which can be used to derive bounds on the expected regret (i.e., additive loss with respect to a benchmark) for any online policy and offline benchmark; Second, using this technique, we show that the Bayes Selector has constant expected regret (i.e., independent of the number of arrivals and resource levels) in any online packing and matching problem with a finite type-space. Our results generalize and simplify many existing results for online packing and matching problems, and suggest a promising pathway for obtaining oracle-driven policies for other online decision-making settings.