Alberto De Luca
Automatic, fast and robust characterization of noise distributions for diffusion MRI
Oct 02, 2018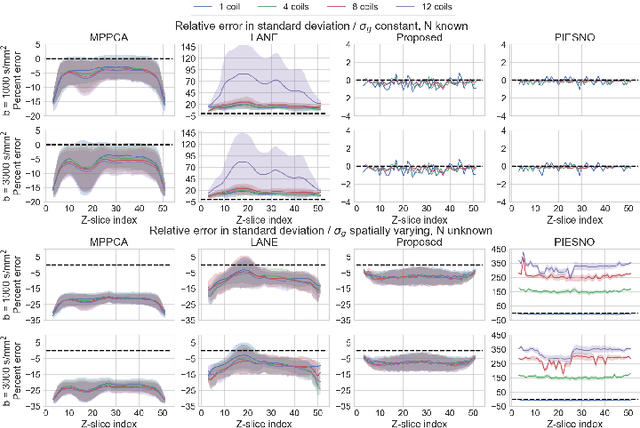
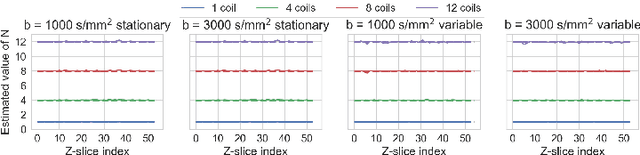
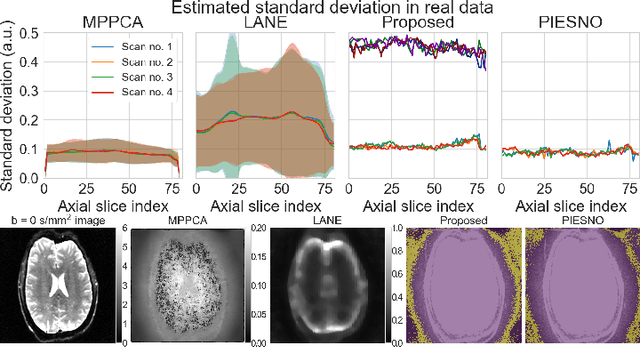
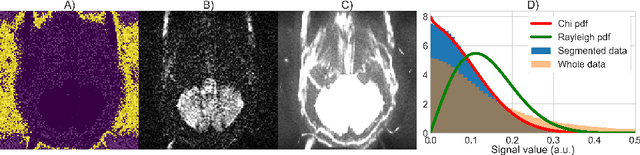
Abstract:Knowledge of the noise distribution in magnitude diffusion MRI images is the centerpiece to quantify uncertainties arising from the acquisition process. The use of parallel imaging methods, the number of receiver coils and imaging filters applied by the scanner, amongst other factors, dictate the resulting signal distribution. Accurate estimation beyond textbook Rician or noncentral chi distributions often requires information about the acquisition process (e.g. coils sensitivity maps or reconstruction coefficients), which is not usually available. We introduce a new method where a change of variable naturally gives rise to a particular form of the gamma distribution for background signals. The first moments and maximum likelihood estimators of this gamma distribution explicitly depend on the number of coils, making it possible to estimate all unknown parameters using only the magnitude data. A rejection step is used to make the method automatic and robust to artifacts. Experiments on synthetic datasets show that the proposed method can reliably estimate both the degrees of freedom and the standard deviation. The worst case errors range from below 2% (spatially uniform noise) to approximately 10% (spatially variable noise). Repeated acquisitions of in vivo datasets show that the estimated parameters are stable and have lower variances than compared methods.
* v2: added publisher DOI statement, fixed text typo in appendix A2
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge