Real-time elastic partial shape matching using a neural network-based adjoint method

Surface matching usually provides significant deformations that can lead to structural failure due to the lack of physical policy. In this context, partial surface matching of non-linear deformable bodies is crucial in engineering to govern structure deformations. In this article, we propose to formulate the registration problem as an optimal control problem using an artificial neural network where the unknown is the surface force distribution that applies to the object and the resulting deformation computed using a hyper-elastic model. The optimization problem is solved using an adjoint method where the hyper-elastic problem is solved using the feed-forward neural network and the adjoint problem is obtained through the backpropagation of the network. Our process improves the computation speed by multiple orders of magnitude while providing acceptable registration errors.

DeepPhysics: a physics aware deep learning framework for real-time simulation

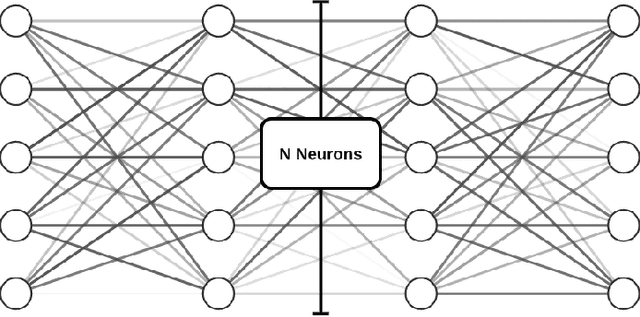
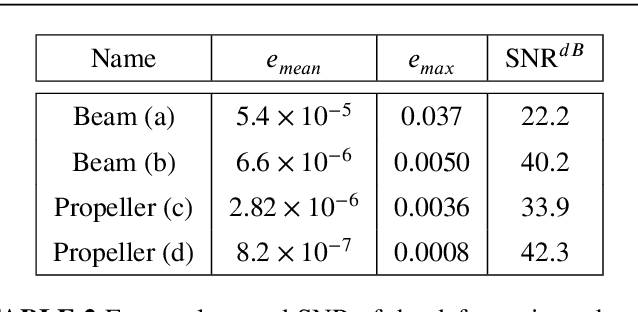
Real-time simulation of elastic structures is essential in many applications, from computer-guided surgical interventions to interactive design in mechanical engineering. The Finite Element Method is often used as the numerical method of reference for solving the partial differential equations associated with these problems. Yet, deep learning methods have recently shown that they could represent an alternative strategy to solve physics-based problems 1,2,3. In this paper, we propose a solution to simulate hyper-elastic materials using a data-driven approach, where a neural network is trained to learn the non-linear relationship between boundary conditions and the resulting displacement field. We also introduce a method to guarantee the validity of the solution. In total, we present three contributions: an optimized data set generation algorithm based on modal analysis, a physics-informed loss function, and a Hybrid Newton-Raphson algorithm. The method is applied to two benchmarks: a cantilever beam and a propeller. The results show that our network architecture trained with a limited amount of data can predict the displacement field in less than a millisecond. The predictions on various geometries, topologies, mesh resolutions, and boundary conditions are accurate to a few micrometers for non-linear deformations of several centimeters of amplitude.