ZipMPC: Compressed Context-Dependent MPC Cost via Imitation Learning

The computational burden of model predictive control (MPC) limits its application on real-time systems, such as robots, and often requires the use of short prediction horizons. This not only affects the control performance, but also increases the difficulty of designing MPC cost functions that reflect the desired long-term objective. This paper proposes ZipMPC, a method that imitates a long-horizon MPC behaviour by learning a compressed and context-dependent cost function for a short-horizon MPC. It improves performance over alternative methods, such as approximate explicit MPC and automatic cost parameter tuning, in particular in terms of i) optimizing the long term objective; ii) maintaining computational costs comparable to a short-horizon MPC; iii) ensuring constraint satisfaction; and iv) generalizing control behaviour to environments not observed during training. For this purpose, ZipMPC leverages the concept of differentiable MPC with neural networks to propagate gradients of the imitation loss through the MPC optimization. We validate our proposed method in simulation and real-world experiments on autonomous racing. ZipMPC consistently completes laps faster than selected baselines, achieving lap times close to the long-horizon MPC baseline. In challenging scenarios where the short-horizon MPC baseline fails to complete a lap, ZipMPC is able to do so. In particular, these performance gains are also observed on tracks unseen during training.

Learning Solutions of Stochastic Optimization Problems with Bayesian Neural Networks

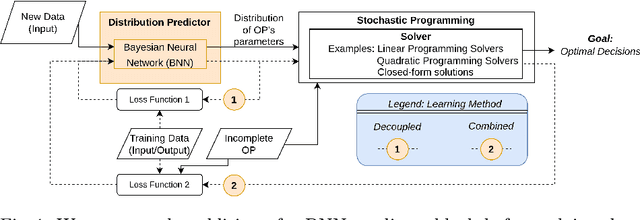
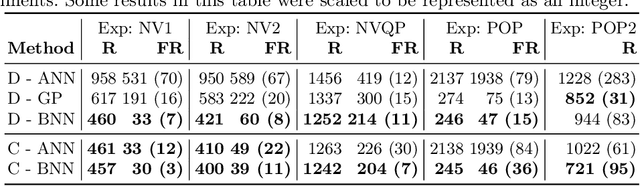
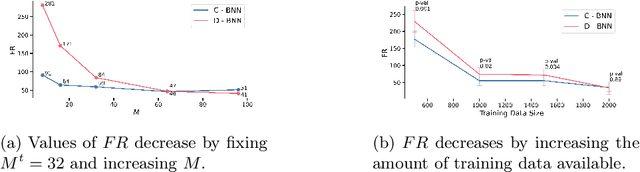
Mathematical solvers use parametrized Optimization Problems (OPs) as inputs to yield optimal decisions. In many real-world settings, some of these parameters are unknown or uncertain. Recent research focuses on predicting the value of these unknown parameters using available contextual features, aiming to decrease decision regret by adopting end-to-end learning approaches. However, these approaches disregard prediction uncertainty and therefore make the mathematical solver susceptible to provide erroneous decisions in case of low-confidence predictions. We propose a novel framework that models prediction uncertainty with Bayesian Neural Networks (BNNs) and propagates this uncertainty into the mathematical solver with a Stochastic Programming technique. The differentiable nature of BNNs and differentiable mathematical solvers allow for two different learning approaches: In the Decoupled learning approach, we update the BNN weights to increase the quality of the predictions' distribution of the OP parameters, while in the Combined learning approach, we update the weights aiming to directly minimize the expected OP's cost function in a stochastic end-to-end fashion. We do an extensive evaluation using synthetic data with various noise properties and a real dataset, showing that decisions regret are generally lower (better) with both proposed methods.

DataSP: A Differential All-to-All Shortest Path Algorithm for Learning Costs and Predicting Paths with Context

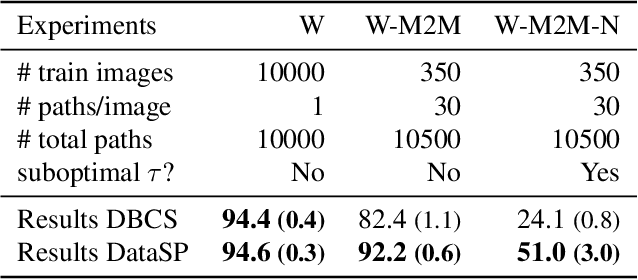
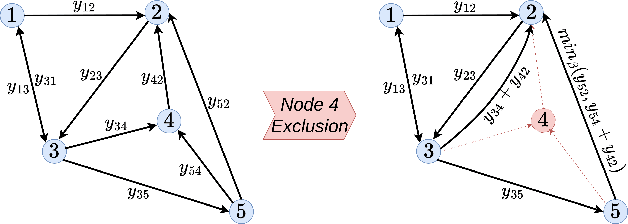
Learning latent costs of transitions on graphs from trajectories demonstrations under various contextual features is challenging but useful for path planning. Yet, existing methods either oversimplify cost assumptions or scale poorly with the number of observed trajectories. This paper introduces DataSP, a differentiable all-to-all shortest path algorithm to facilitate learning latent costs from trajectories. It allows to learn from a large number of trajectories in each learning step without additional computation. Complex latent cost functions from contextual features can be represented in the algorithm through a neural network approximation. We further propose a method to sample paths from DataSP in order to reconstruct/mimic observed paths' distributions. We prove that the inferred distribution follows the maximum entropy principle. We show that DataSP outperforms state-of-the-art differentiable combinatorial solver and classical machine learning approaches in predicting paths on graphs.