Adaptive Random Fourier Features Training Stabilized By Resampling With Applications in Image Regression

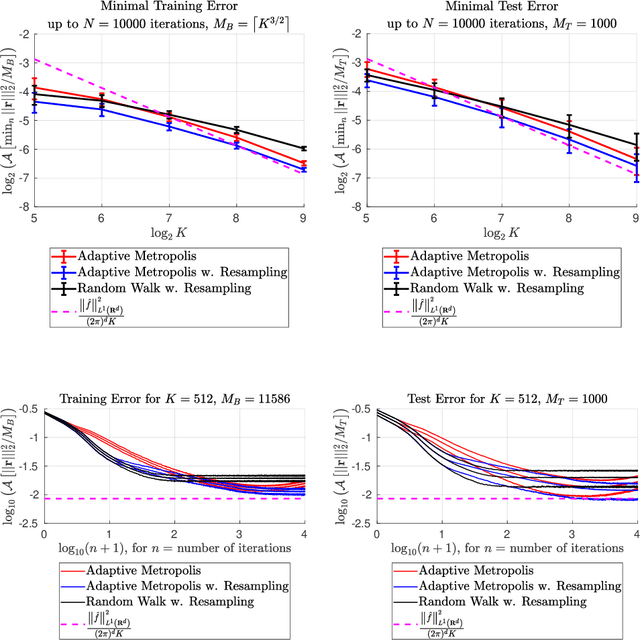
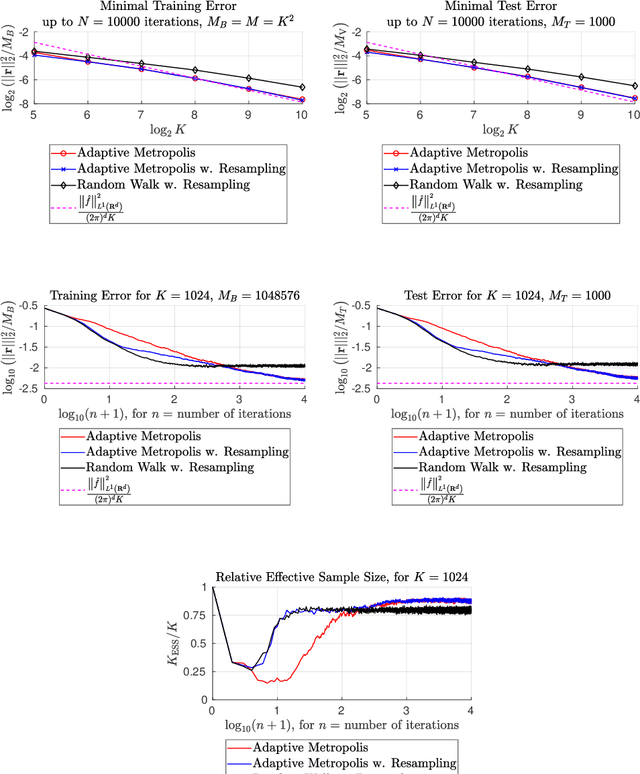
This paper presents an enhanced adaptive random Fourier features (ARFF) training algorithm for shallow neural networks, building upon the work introduced in "Adaptive Random Fourier Features with Metropolis Sampling", Kammonen et al., Foundations of Data Science, 2(3):309--332, 2020. This improved method uses a particle filter type resampling technique to stabilize the training process and reduce sensitivity to parameter choices. With resampling, the Metropolis test may also be omitted, reducing the number of hyperparameters and reducing the computational cost per iteration, compared to ARFF. We present comprehensive numerical experiments demonstrating the efficacy of our proposed algorithm in function regression tasks, both as a standalone method and as a pre-training step before gradient-based optimization, here Adam. Furthermore, we apply our algorithm to a simple image regression problem, showcasing its utility in sampling frequencies for the random Fourier features (RFF) layer of coordinate-based multilayer perceptrons (MLPs). In this context, we use the proposed algorithm to sample the parameters of the RFF layer in an automated manner.

Comparing Spectral Bias and Robustness For Two-Layer Neural Networks: SGD vs Adaptive Random Fourier Features

We present experimental results highlighting two key differences resulting from the choice of training algorithm for two-layer neural networks. The spectral bias of neural networks is well known, while the spectral bias dependence on the choice of training algorithm is less studied. Our experiments demonstrate that an adaptive random Fourier features algorithm (ARFF) can yield a spectral bias closer to zero compared to the stochastic gradient descent optimizer (SGD). Additionally, we train two identically structured classifiers, employing SGD and ARFF, to the same accuracy levels and empirically assess their robustness against adversarial noise attacks.