Deep Graph Attention Networks

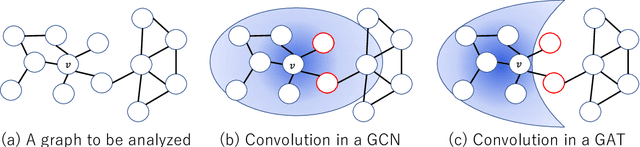
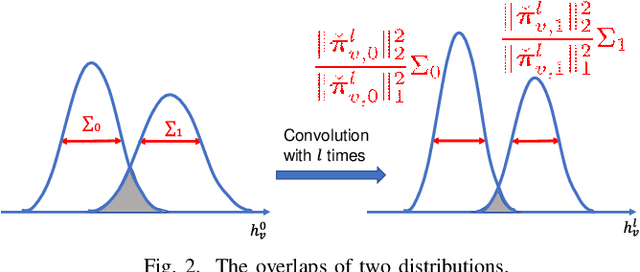
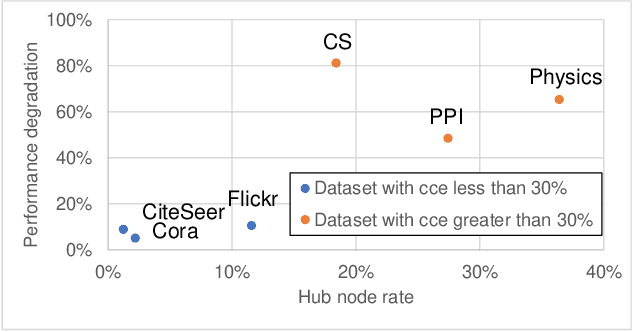
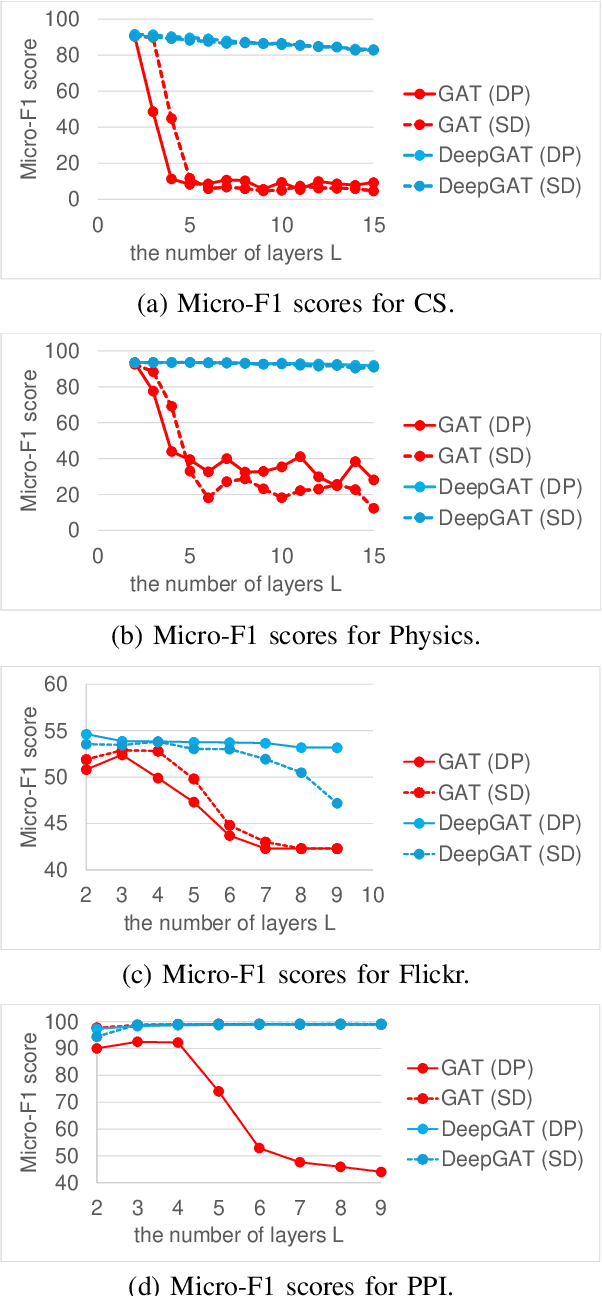
Graphs are useful for representing various realworld objects. However, graph neural networks (GNNs) tend to suffer from over-smoothing, where the representations of nodes of different classes become similar as the number of layers increases, leading to performance degradation. A method that does not require protracted tuning of the number of layers is needed to effectively construct a graph attention network (GAT), a type of GNN. Therefore, we introduce a method called "DeepGAT" for predicting the class to which nodes belong in a deep GAT. It avoids over-smoothing in a GAT by ensuring that nodes in different classes are not similar at each layer. Using DeepGAT to predict class labels, a 15-layer network is constructed without the need to tune the number of layers. DeepGAT prevented over-smoothing and achieved a 15-layer GAT with similar performance to a 2-layer GAT, as indicated by the similar attention coefficients. DeepGAT enables the training of a large network to acquire similar attention coefficients to a network with few layers. It avoids the over-smoothing problem and obviates the need to tune the number of layers, thus saving time and enhancing GNN performance.

Refining Similarity Matrices to Cluster Attributed Networks Accurately

As a result of the recent popularity of social networks and the increase in the number of research papers published across all fields, attributed networks consisting of relationships between objects, such as humans and the papers, that have attributes are becoming increasingly large. Therefore, various studies for clustering attributed networks into sub-networks are being actively conducted. When clustering attributed networks using spectral clustering, the clustering accuracy is strongly affected by the quality of the similarity matrices, which are input into spectral clustering and represent the similarities between pairs of objects. In this paper, we aim to increase the accuracy by refining the matrices before applying spectral clustering to them. We verify the practicability of our proposed method by comparing the accuracy of spectral clustering with similarity matrices before and after refining them.