DADAgger: Disagreement-Augmented Dataset Aggregation

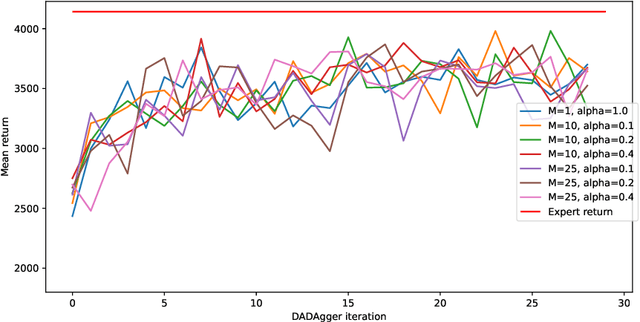
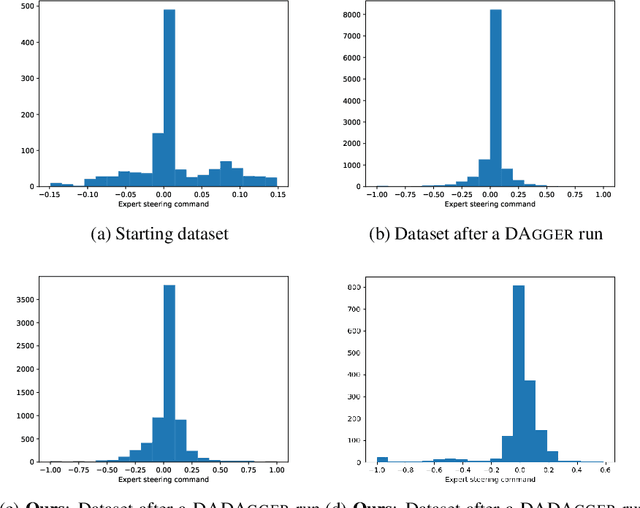
DAgger is an imitation algorithm that aggregates its original datasets by querying the expert on all samples encountered during training. In order to reduce the number of samples queried, we propose a modification to DAgger, known as DADAgger, which only queries the expert for state-action pairs that are out of distribution (OOD). OOD states are identified by measuring the variance of the action predictions of an ensemble of models on each state, which we simulate using dropout. Testing on the Car Racing and Half Cheetah environments achieves comparable performance to DAgger but with reduced expert queries, and better performance than a random sampling baseline. We also show that our algorithm may be used to build efficient, well-balanced training datasets by running with no initial data and only querying the expert to resolve uncertainty.

Deep Neural Networks to Correct Sub-Precision Errors in CFD

Loss of information in numerical simulations can arise from various sources while solving discretized partial differential equations. In particular, precision-related errors can accumulate in the quantities of interest when the simulations are performed using low-precision 16-bit floating-point arithmetic compared to an equivalent 64-bit simulation. Here, low-precision computation requires much lower resources than high-precision computation. Several machine learning (ML) techniques proposed recently have been successful in correcting the errors arising from spatial discretization. In this work, we extend these techniques to improve Computational Fluid Dynamics (CFD) simulations performed using low numerical precision. We first quantify the precision related errors accumulated in a Kolmogorov forced turbulence test case. Subsequently, we employ a Convolutional Neural Network together with a fully differentiable numerical solver performing 16-bit arithmetic to learn a tightly-coupled ML-CFD hybrid solver. Compared to the 16-bit solver, we demonstrate the efficacy of the ML-CFD hybrid solver towards reducing the error accumulation in the velocity field and improving the kinetic energy spectrum at higher frequencies.