Ahmed Youssef
Hacking Generative Models with Differentiable Network Bending
Oct 07, 2023



Abstract:In this work, we propose a method to 'hack' generative models, pushing their outputs away from the original training distribution towards a new objective. We inject a small-scale trainable module between the intermediate layers of the model and train it for a low number of iterations, keeping the rest of the network frozen. The resulting output images display an uncanny quality, given by the tension between the original and new objectives that can be exploited for artistic purposes.
Limiting fitness distributions in evolutionary dynamics
Feb 16, 2016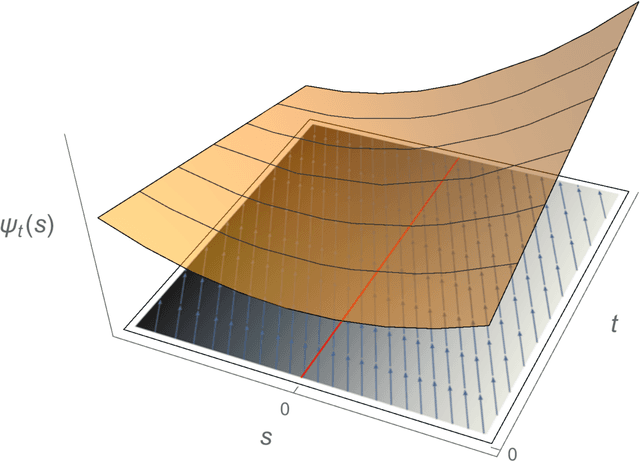
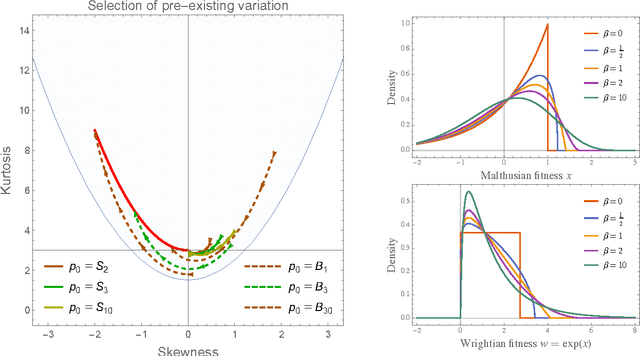
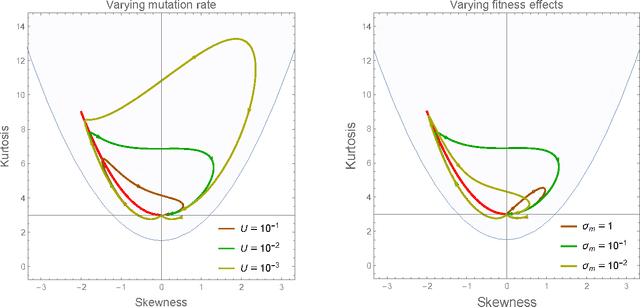
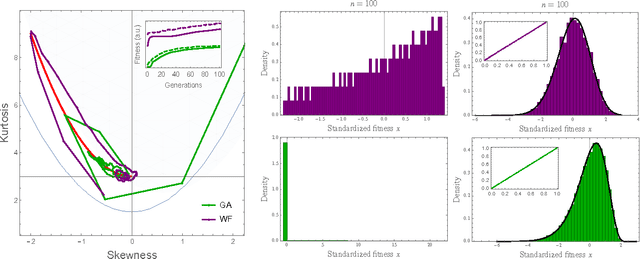
Abstract:Darwinian evolution can be modeled in general terms as a flow in the space of fitness (i.e. reproductive rate) distributions. In the diffusion approximation, Tsimring et al. have showed that this flow admits "fitness wave" solutions: Gaussian-shape fitness distributions moving towards higher fitness values at constant speed. Here we show more generally that evolving fitness distributions are attracted to a one-parameter family of distributions with a fixed parabolic relationship between skewness and kurtosis. Unlike fitness waves, this statistical pattern encompasses both positive and negative (a.k.a. purifying) selection and is not restricted to rapidly adapting populations. Moreover we find that the mean fitness of a population under the selection of pre-existing variation is a power-law function of time, as observed in microbiological evolution experiments but at variance with fitness wave theory. At the conceptual level, our results can be viewed as the resolution of the "dynamic insufficiency" of Fisher's fundamental theorem of natural selection. Our predictions are in good agreement with numerical simulations.
* 15 pages + appendices
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge