Weighted Random Search for Hyperparameter Optimization

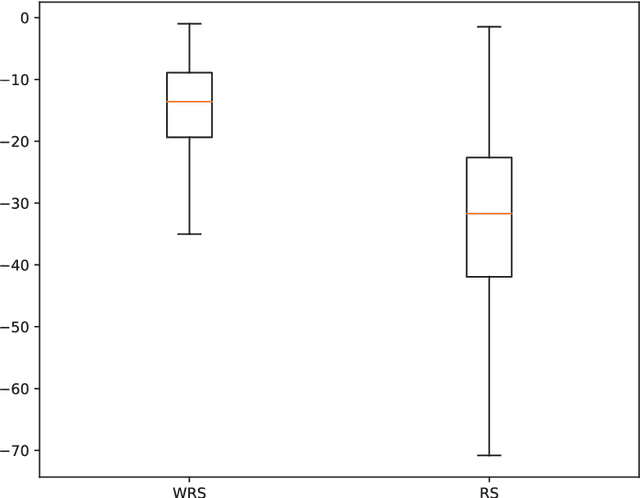
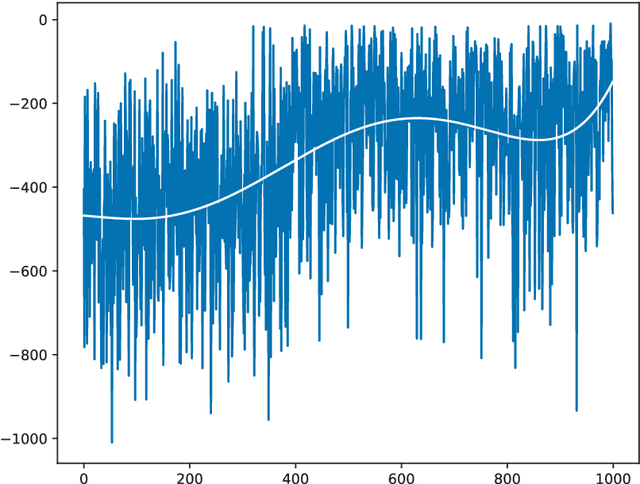
We introduce an improved version of Random Search (RS), used here for hyperparameter optimization of machine learning algorithms. Unlike the standard RS, which generates for each trial new values for all hyperparameters, we generate new values for each hyperparameter with a probability of change. The intuition behind our approach is that a value that already triggered a good result is a good candidate for the next step, and should be tested in new combinations of hyperparameter values. Within the same computational budget, our method yields better results than the standard RS. Our theoretical results prove this statement. We test our method on a variation of one of the most commonly used objective function for this class of problems (the Grievank function) and for the hyperparameter optimization of a deep learning CNN architecture. Our results can be generalized to any optimization problem defined on a discrete domain.

Weighted Random Search for CNN Hyperparameter Optimization

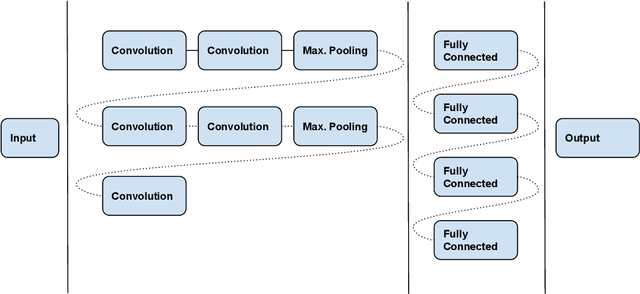
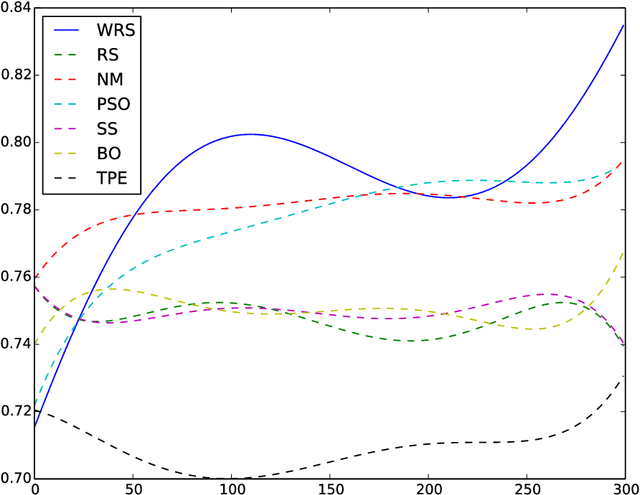
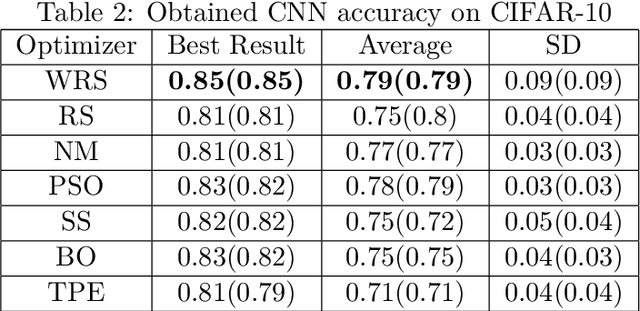
Nearly all model algorithms used in machine learning use two different sets of parameters: the training parameters and the meta-parameters (hyperparameters). While the training parameters are learned during the training phase, the values of the hyperparameters have to be specified before learning starts. For a given dataset, we would like to find the optimal combination of hyperparameter values, in a reasonable amount of time. This is a challenging task because of its computational complexity. In previous work [11], we introduced the Weighted Random Search (WRS) method, a combination of Random Search (RS) and probabilistic greedy heuristic. In the current paper, we compare the WRS method with several state-of-the art hyperparameter optimization methods with respect to Convolutional Neural Network (CNN) hyperparameter optimization. The criterion is the classification accuracy achieved within the same number of tested combinations of hyperparameter values. According to our experiments, the WRS algorithm outperforms the other methods.