Adrián Lozano-Durán
Computational model discovery with reinforcement learning
Dec 29, 2019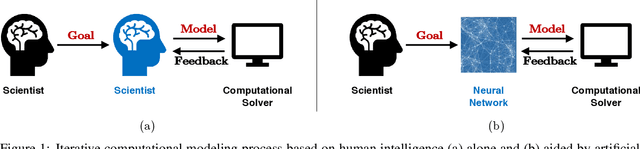
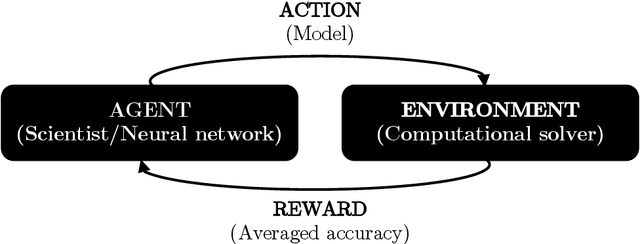
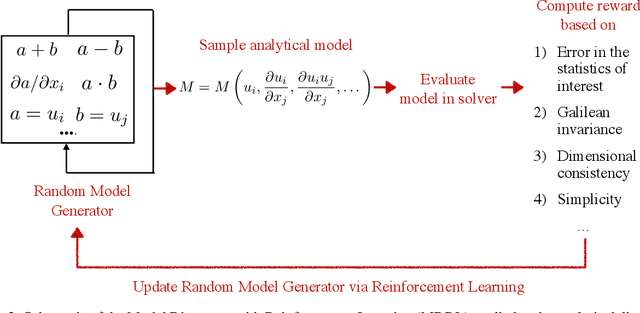

Abstract:The motivation of this study is to leverage recent breakthroughs in artificial intelligence research to unlock novel solutions to important scientific problems encountered in computational science. To address the human intelligence limitations in discovering reduced-order models, we propose to supplement human thinking with artificial intelligence. Our three-pronged strategy consists of learning (i) models expressed in analytical form, (ii) which are evaluated a posteriori, and iii) using exclusively integral quantities from the reference solution as prior knowledge. In point (i), we pursue interpretable models expressed symbolically as opposed to black-box neural networks, the latter only being used during learning to efficiently parameterize the large search space of possible models. In point (ii), learned models are dynamically evaluated a posteriori in the computational solver instead of based on a priori information from preprocessed high-fidelity data, thereby accounting for the specificity of the solver at hand such as its numerics. Finally in point (iii), the exploration of new models is solely guided by predefined integral quantities, e.g., averaged quantities of engineering interest in Reynolds-averaged or large-eddy simulations (LES). We use a coupled deep reinforcement learning framework and computational solver to concurrently achieve these objectives. The combination of reinforcement learning with objectives (i), (ii) and (iii) differentiate our work from previous modeling attempts based on machine learning. In this report, we provide a high-level description of the model discovery framework with reinforcement learning. The method is detailed for the application of discovering missing terms in differential equations. An elementary instantiation of the method is described that discovers missing terms in the Burgers' equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge