A greedy anytime algorithm for sparse PCA

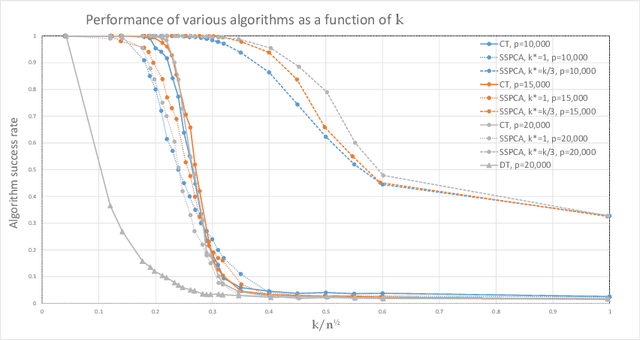
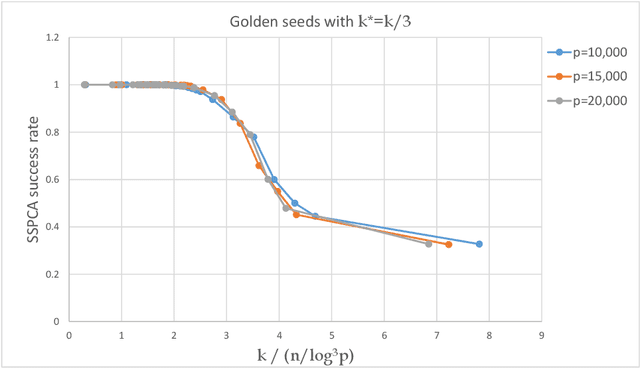
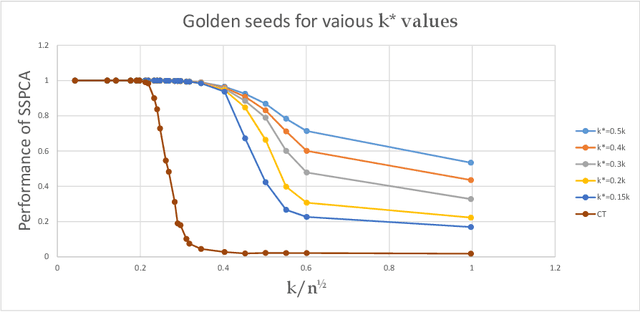
The taxing computational effort that is involved in solving some high-dimensional statistical problems, in particular problems involving non-convex optimization, has popularized the development and analysis of algorithms that run efficiently (polynomial-time) but with no general guarantee on statistical consistency. In light of the ever-increasing compute power and decreasing costs, perhaps a more useful characterization of algorithms is by their ability to calibrate the invested computational effort with the statistical features of the input at hand. For example, design an algorithm that always guarantees consistency by increasing the run-time as the SNR weakens. We exemplify this principle in the $\ell_0$-sparse PCA problem. We propose a new greedy algorithm to solve sparse PCA that supports such a calibration. We analyze it in the well-known spiked-covariance model for various SNR regimes. In particular, our findings suggest that our algorithm recovers the spike in SNR regimes where all polynomial-time algorithms fail, while running much faster than the naive exhaustive search.