Graph Vertex Embeddings: Distance, Regularization and Community Detection

Graph embeddings have emerged as a powerful tool for representing complex network structures in a low-dimensional space, enabling the use of efficient methods that employ the metric structure in the embedding space as a proxy for the topological structure of the data. In this paper, we explore several aspects that affect the quality of a vertex embedding of graph-structured data. To this effect, we first present a family of flexible distance functions that faithfully capture the topological distance between different vertices. Secondly, we analyze vertex embeddings as resulting from a fitted transformation of the distance matrix rather than as a direct result of optimization. Finally, we evaluate the effectiveness of our proposed embedding constructions by performing community detection on a host of benchmark datasets. The reported results are competitive with classical algorithms that operate on the entire graph while benefitting from a substantially reduced computational complexity due to the reduced dimensionality of the representations.

Graph autoencoder with constant dimensional latent space

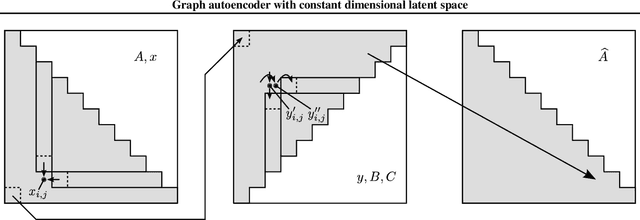
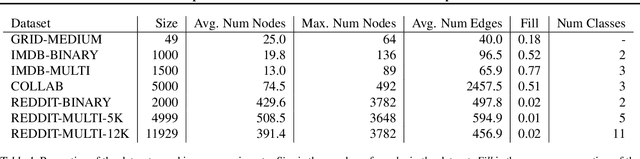
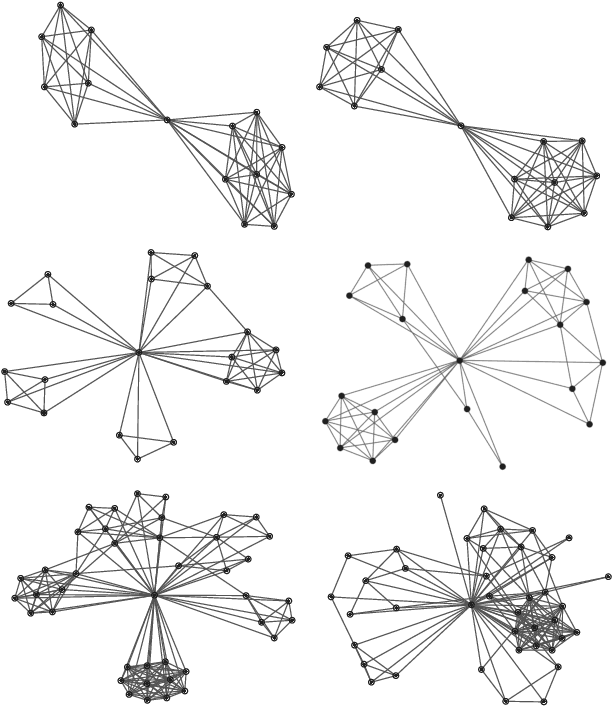
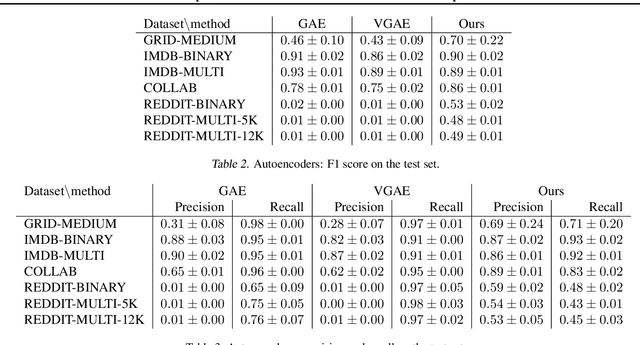
Invertible transformation of large graphs into constant dimensional vectors (embeddings) remains a challenge. In this paper we address it with recursive neural networks: The encoder and the decoder. The encoder network transforms embeddings of subgraphs into embeddings of larger subgraphs, and eventually into the embedding of the input graph. The decoder does the opposite. The dimension of the embeddings is constant regardless of the size of the (sub)graphs. Simulation experiments presented in this paper confirm that our proposed graph autoencoder can handle graphs with even thousands of vertices.