Robust Nonprehensile Object Transportation with Uncertain Inertial Parameters

We consider the nonprehensile object transportation task known as the waiter's problem - in which a robot must move an object balanced on a tray from one location to another - when the balanced object has uncertain inertial parameters. In contrast to existing approaches that completely ignore uncertainty in the inertia matrix or which only consider small parameter errors, we are interested in pushing the limits of the amount of inertial parameter uncertainty that can be handled. We first show how balancing constraints robust to inertial parameter uncertainty can be incorporated into a motion planning framework to balance objects while moving quickly. Next, we develop necessary conditions for the inertial parameters to be realizable on a bounding shape based on moment relaxations, allowing us to verify whether a trajectory will violate the balancing constraints for any realizable inertial parameters. Finally, we demonstrate our approach on a mobile manipulator in simulations and real hardware experiments: our proposed robust constraints consistently balance a 56 cm tall object with substantial inertial parameter uncertainty in the real world, while the baseline approaches drop the object while transporting it.

Force Push: Robust Single-Point Pushing with Force Feedback

We present the first controller for quasistatic robotic planar pushing with single-point contact using only force feedback. We consider an omnidirectional mobile robot pushing an object (the "slider") along a given path, where the robot is equipped with a force-torque sensor to measure the force at the contact point with the slider. The geometric, inertial, and frictional parameters of the slider are not known to the controller, nor are measurements of the slider's pose. We assume that the robot can be localized so that the global position of the contact point is always known and that the approximate initial position of the slider is provided. Simulations and real-world experiments show that our controller yields stable pushes that are robust to a wide range of slider parameters and state perturbations along both straight and curved paths. Furthermore, we use an admittance controller to adjust the pushing velocity based on the measured force when the slider contacts obstacles like walls.

Keep it Upright: Model Predictive Control for Nonprehensile Object Transportation with Obstacle Avoidance on a Mobile Manipulator

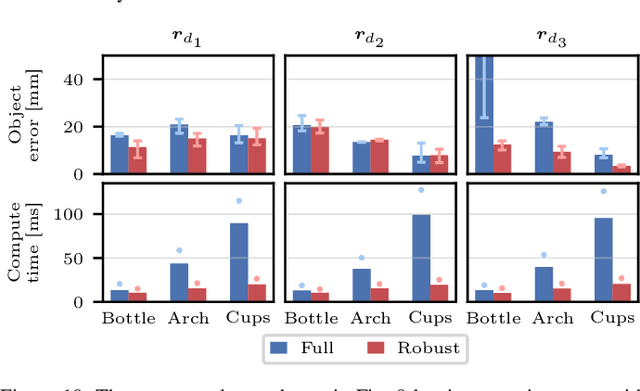
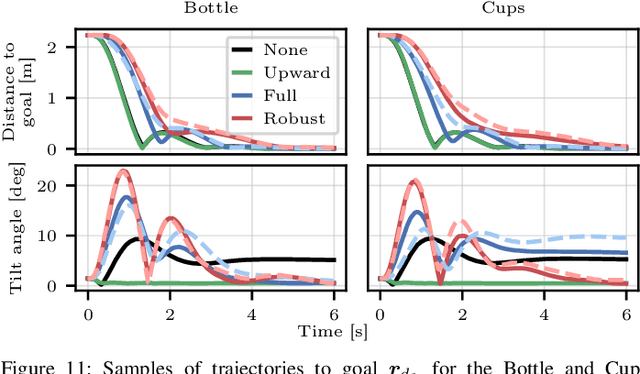
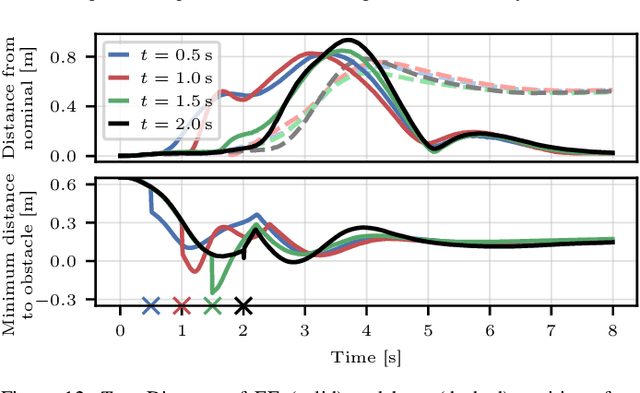
We consider a nonprehensile manipulation task in which a mobile manipulator must balance objects on its end effector without grasping them -- known as the waiter's problem -- and move to a desired location while avoiding static and dynamic obstacles. In constrast to existing approaches, our focus is on fast online planning in response to new and changing environments. Our main contribution is a whole-body constrained model predictive controller (MPC) for a mobile manipulator that balances objects and avoids collisions. Furthermore, we propose planning using the minimum statically-feasible friction coefficients, which provides robustness to frictional uncertainty and other force disturbances while also substantially reducing the compute time required to update the MPC policy. Simulations and hardware experiments on a velocity-controlled mobile manipulator with up to seven balanced objects, stacked objects, and various obstacles show that our approach can handle a variety of conditions that have not been previously demonstrated, with end effector speeds and accelerations up to 2.0 m/s and 7.9 m/s$^2$, respectively. Notably, we demonstrate a projectile avoidance task in which the robot avoids a thrown ball while balancing a tall bottle.

Robust Single-Point Pushing with Force Feedback

We present the first controller for quasistatic robotic planar pushing with single-point contact using only force feedback. We consider a mobile robot equipped with a force-torque sensor to measure the force at the contact point with the pushed object (the "slider"). The parameters of the slider are not known to the controller, nor is feedback on the slider's pose. We assume that the global position of the contact point is always known and that the approximate initial position of the slider is provided. We focus specifically on the case when it is desired to push the slider along a straight line. Simulations and real-world experiments show that our controller yields stable pushes that are robust to a wide range of slider parameters and state perturbations.

Provably Robust Learning-Based Approach for High-Accuracy Tracking Control of Lagrangian Systems

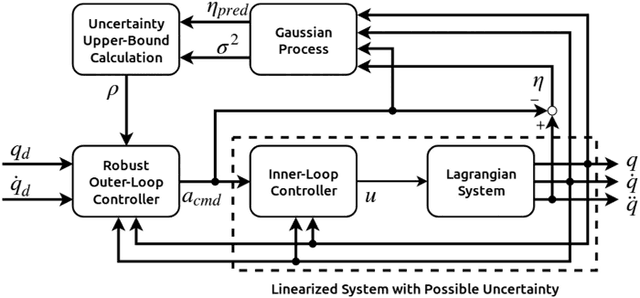
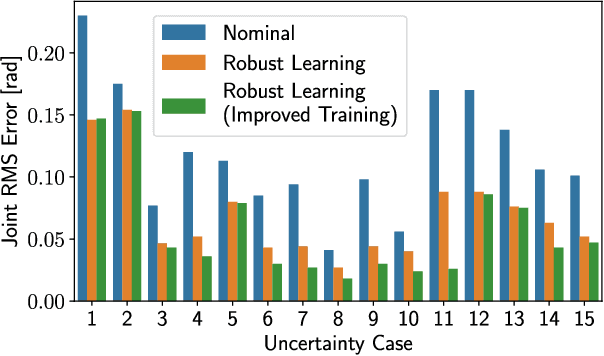
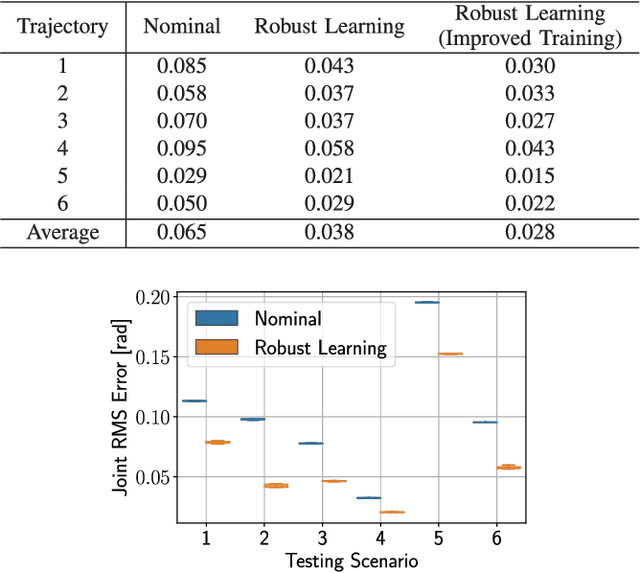
Lagrangian systems represent a wide range of robotic systems, including manipulators, wheeled and legged robots, and quadrotors. Inverse dynamics control and feedforward linearization techniques are typically used to convert the complex nonlinear dynamics of Lagrangian systems to a set of decoupled double integrators, and then a standard, outer-loop controller can be used to calculate the commanded acceleration for the linearized system. However, these methods typically depend on having a very accurate system model, which is often not available in practice. While this challenge has been addressed in the literature using different learning approaches, most of these approaches do not provide safety guarantees in terms of stability of the learning-based control system. In this paper, we provide a novel, learning-based control approach based on Gaussian processes (GPs) that ensures both stability of the closed-loop system and high-accuracy tracking. We use GPs to approximate the error between the commanded acceleration and the actual acceleration of the system, and then use the predicted mean and variance of the GP to calculate an upper bound on the uncertainty of the linearized model. This uncertainty bound is then used in a robust, outer-loop controller to ensure stability of the overall system. Moreover, we show that the tracking error converges to a ball with a radius that can be made arbitrarily small. Furthermore, we verify the effectiveness of our approach via simulations on a 2 degree-of-freedom (DOF) planar manipulator and experimentally on a 6 DOF industrial manipulator.