From Observation to Orientation: an Adaptive Integer Programming Approach to Intervention Design

Using both observational and experimental data, a causal discovery process can identify the causal relationships between variables. A unique adaptive intervention design paradigm is presented in this work, where causal directed acyclic graphs (DAGs) are for effectively recovered with practical budgetary considerations. In order to choose treatments that optimize information gain under these considerations, an iterative integer programming (IP) approach is proposed, which drastically reduces the number of experiments required. Simulations over a broad range of graph sizes and edge densities are used to assess the effectiveness of the suggested approach. Results show that the proposed adaptive IP approach achieves full causal graph recovery with fewer intervention iterations and variable manipulations than random intervention baselines, and it is also flexible enough to accommodate a variety of practical constraints.

Causal Discovery by Interventions via Integer Programming

Causal discovery is essential across various scientific fields to uncover causal structures within data. Traditional methods relying on observational data have limitations due to confounding variables. This paper presents an optimization-based approach using integer programming (IP) to design minimal intervention sets that ensure causal structure identifiability. Our method provides exact and modular solutions that can be adjusted to different experimental settings and constraints. We demonstrate its effectiveness through comparative analysis across different settings, demonstrating its applicability and robustness.

MEC-IP: Efficient Discovery of Markov Equivalent Classes via Integer Programming

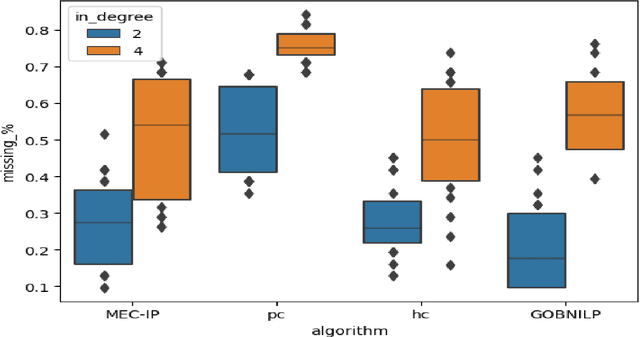
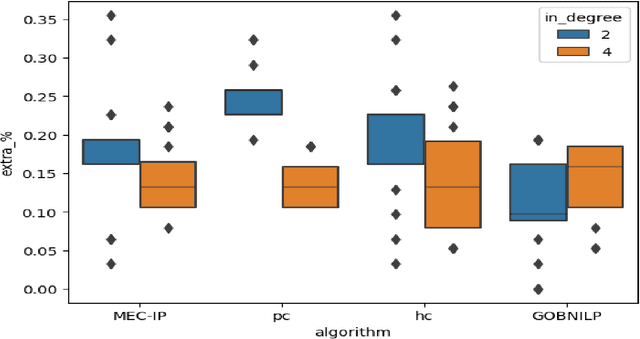
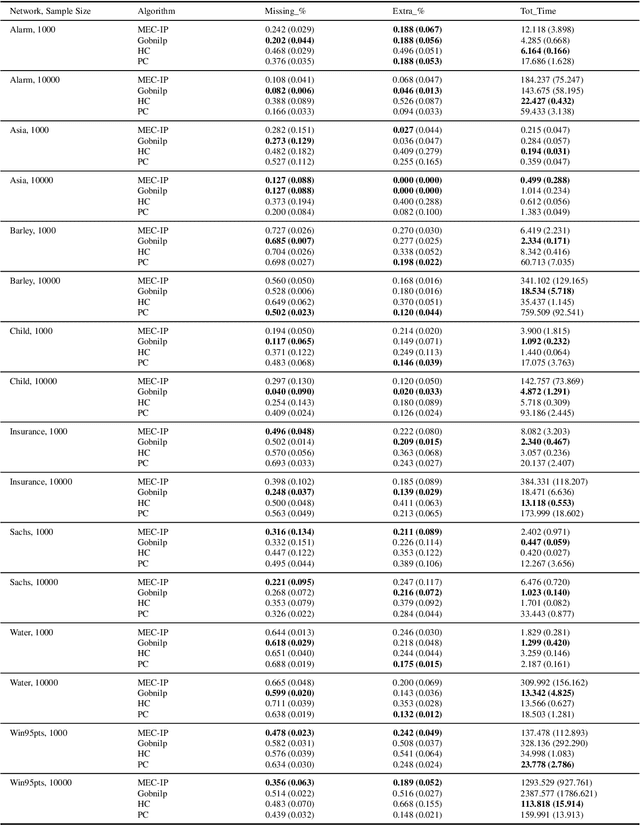
This paper presents a novel Integer Programming (IP) approach for discovering the Markov Equivalent Class (MEC) of Bayesian Networks (BNs) through observational data. The MEC-IP algorithm utilizes a unique clique-focusing strategy and Extended Maximal Spanning Graphs (EMSG) to streamline the search for MEC, thus overcoming the computational limitations inherent in other existing algorithms. Our numerical results show that not only a remarkable reduction in computational time is achieved by our algorithm but also an improvement in causal discovery accuracy is seen across diverse datasets. These findings underscore this new algorithm's potential as a powerful tool for researchers and practitioners in causal discovery and BNSL, offering a significant leap forward toward the efficient and accurate analysis of complex data structures.