Trajectory Reconstruction through a Gaussian Adaptive Selective Outlier Rejecting Smoother

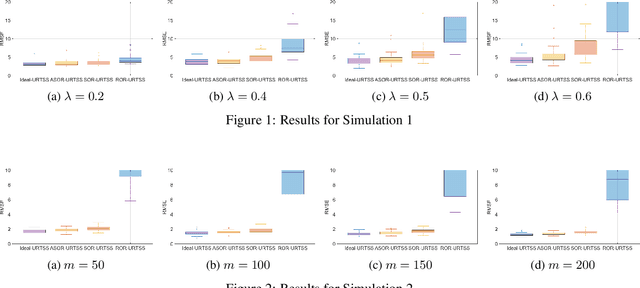
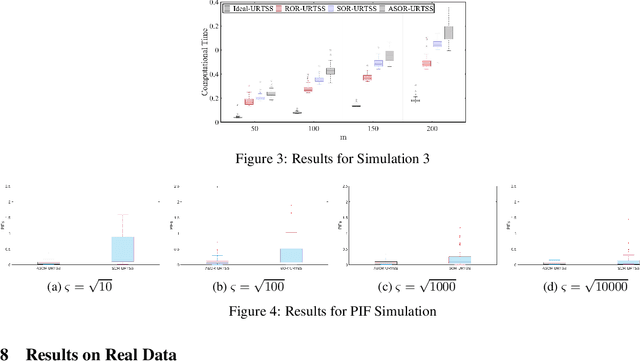
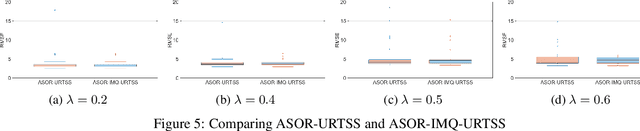
Trajectory Reconstruction (TR) is vital for accurately mapping movement patterns and validating analyses, especially in fields like robotics, biomechanics, and environmental tracking, where data might be missing or affected by outliers. Improving Trajectory estimation by employing Gaussian smoothing techniques in the presence of non-Gaussian noise is the subject of this work. We consider the case where data is collected from independent sensors. A variational Bayesian (VB) based Unscented Raunch-Tung-Striebel smoothing (URTSS) scheme is proposed which adopts a vectorized weighing mechanism for the measurement covariance matrix to selectively remove contaminated measurements at each time step. To improve our outlier mitigation, we model our outlier characteristics as a Gamma distribution and dynamically learn the parameters of this distribution from data. We verify the performance of our proposed smoother by a range of simulations and experimental data. We also propose a robustness criterion for smoothers based on the Kullback-Leibler (KL) divergence and show that our proposed method complies with this criterion.

EMORF/S: EM-Based Outlier-Robust Filtering and Smoothing With Correlated Measurement Noise

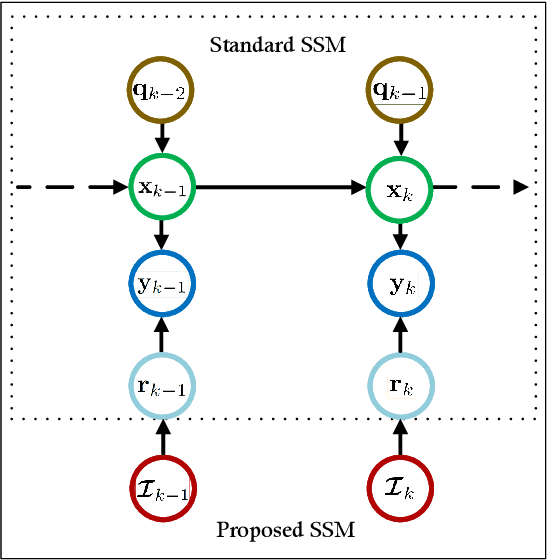
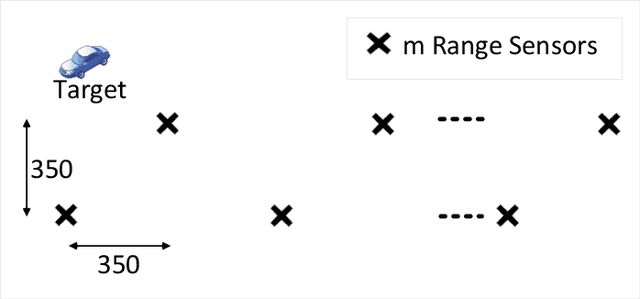
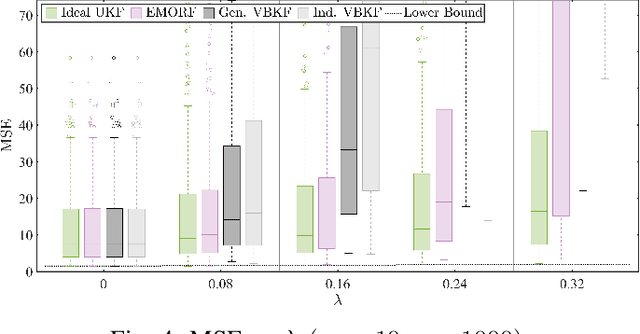
In this article, we consider the problem of outlier-robust state estimation where the measurement noise can be correlated. Outliers in data arise due to many reasons like sensor malfunctioning, environmental behaviors, communication glitches, etc. Moreover, noise correlation emerges in several real-world applications e.g. sensor networks, radar data, GPS-based systems, etc. We consider these effects in system modeling which is subsequently used for inference. We employ the Expectation-Maximization (EM) framework to derive both outlier-resilient filtering and smoothing methods, suitable for online and offline estimation respectively. The standard Gaussian filtering and the Gaussian Rauch-Tung-Striebel (RTS) smoothing results are leveraged to devise the estimators. In addition, Bayesian Cramer-Rao Bounds (BCRBs) for a filter and a smoother which can perfectly detect and reject outliers are presented. These serve as useful theoretical benchmarks to gauge the error performance of different estimators. Lastly, different numerical experiments, for an illustrative target tracking application, are carried out that indicate performance gains compared to similarly engineered state-of-the-art outlier-rejecting state estimators. The advantages are in terms of simpler implementation, enhanced estimation quality, and competitive computational performance.

Bayesian Heuristics for Robust Spatial Perception

Spatial perception is a key task in several robotics applications. In general, it involves the nonlinear estimation of hidden variables that represent the state of the robot/environment. However, in the presence of outliers the standard nonlinear least squared formulation results in poor estimates. Several methods have been considered in the literature to improve the reliability of the estimation process. Most methods are based on heuristics since guaranteed global robust estimation is not generally practical due to high computational costs. Recently general purpose robust estimation heuristics have been proposed that leverage existing non-minimal solvers available for the outlier-free formulations without the need for an initial guess. In this work, we propose two similar heuristics backed by Bayesian theory. We evaluate these heuristics in practical scenarios to demonstrate their merits in different applications including 3D point cloud registration, mesh registration and pose graph optimization.

Outlier-Robust Filtering For Nonlinear Systems With Selective Observations Rejection

This letter presents a novel outlier-robust filter for nonlinear dynamical systems. We consider a common case where measurements are obtained from independent sensors. The proposed method is devised by modifying the measurement model and subsequently using the theory of Variational Bayes and general Gaussian filtering. We treat the measurement outliers independently for independent observations leading to selective rejection of the corrupted observations during inference. By carrying out simulations for variable number of sensors we verify that an implementation of the proposed filter is computationally more efficient as compared to similar baseline methods.