EMORF/S: EM-Based Outlier-Robust Filtering and Smoothing With Correlated Measurement Noise

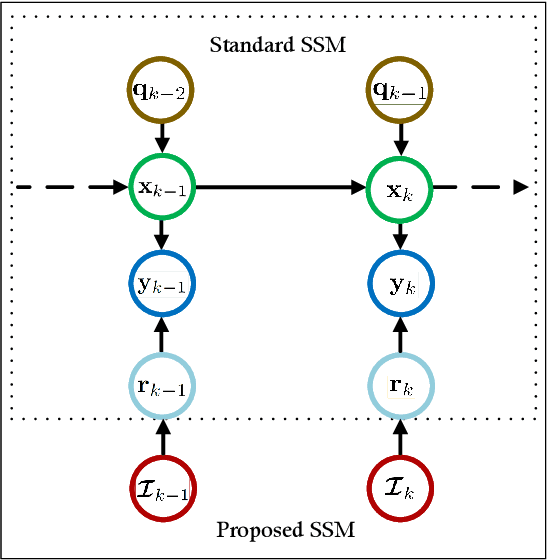
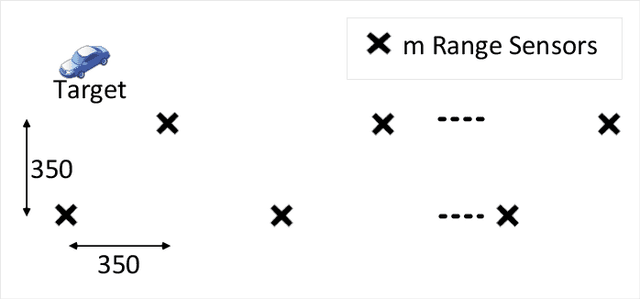
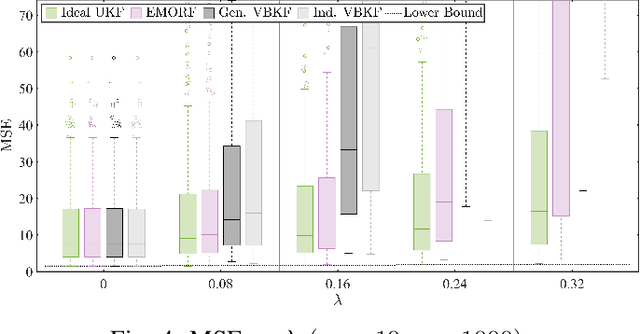
In this article, we consider the problem of outlier-robust state estimation where the measurement noise can be correlated. Outliers in data arise due to many reasons like sensor malfunctioning, environmental behaviors, communication glitches, etc. Moreover, noise correlation emerges in several real-world applications e.g. sensor networks, radar data, GPS-based systems, etc. We consider these effects in system modeling which is subsequently used for inference. We employ the Expectation-Maximization (EM) framework to derive both outlier-resilient filtering and smoothing methods, suitable for online and offline estimation respectively. The standard Gaussian filtering and the Gaussian Rauch-Tung-Striebel (RTS) smoothing results are leveraged to devise the estimators. In addition, Bayesian Cramer-Rao Bounds (BCRBs) for a filter and a smoother which can perfectly detect and reject outliers are presented. These serve as useful theoretical benchmarks to gauge the error performance of different estimators. Lastly, different numerical experiments, for an illustrative target tracking application, are carried out that indicate performance gains compared to similarly engineered state-of-the-art outlier-rejecting state estimators. The advantages are in terms of simpler implementation, enhanced estimation quality, and competitive computational performance.