The Language of Search

This paper is concerned with a class of algorithms that perform exhaustive search on propositional knowledge bases. We show that each of these algorithms defines and generates a propositional language. Specifically, we show that the trace of a search can be interpreted as a combinational circuit, and a search algorithm then defines a propositional language consisting of circuits that are generated across all possible executions of the algorithm. In particular, we show that several versions of exhaustive DPLL search correspond to such well-known languages as FBDD, OBDD, and a precisely-defined subset of d-DNNF. By thus mapping search algorithms to propositional languages, we provide a uniform and practical framework in which successful search techniques can be harnessed for compilation of knowledge into various languages of interest, and a new methodology whereby the power and limitations of search algorithms can be understood by looking up the tractability and succinctness of the corresponding propositional languages.

Complexity Results and Approximation Strategies for MAP Explanations

MAP is the problem of finding a most probable instantiation of a set of variables given evidence. MAP has always been perceived to be significantly harder than the related problems of computing the probability of a variable instantiation Pr, or the problem of computing the most probable explanation (MPE). This paper investigates the complexity of MAP in Bayesian networks. Specifically, we show that MAP is complete for NP^PP and provide further negative complexity results for algorithms based on variable elimination. We also show that MAP remains hard even when MPE and Pr become easy. For example, we show that MAP is NP-complete when the networks are restricted to polytrees, and even then can not be effectively approximated. Given the difficulty of computing MAP exactly, and the difficulty of approximating MAP while providing useful guarantees on the resulting approximation, we investigate best effort approximations. We introduce a generic MAP approximation framework. We provide two instantiations of the framework; one for networks which are amenable to exact inference Pr, and one for networks for which even exact inference is too hard. This allows MAP approximation on networks that are too complex to even exactly solve the easier problems, Pr and MPE. Experimental results indicate that using these approximation algorithms provides much better solutions than standard techniques, and provide accurate MAP estimates in many cases.

A Knowledge Compilation Map

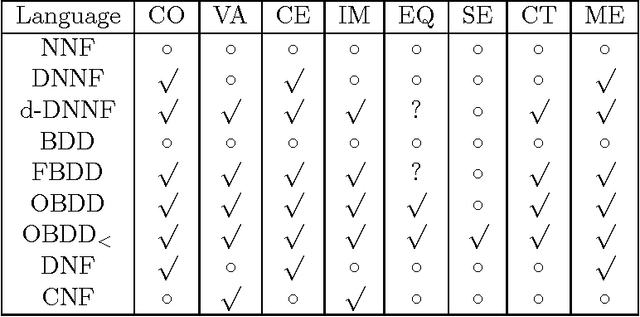
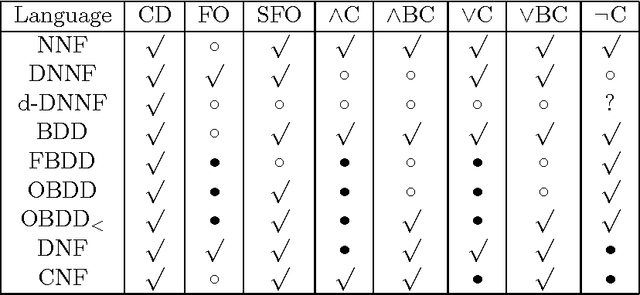
We propose a perspective on knowledge compilation which calls for analyzing different compilation approaches according to two key dimensions: the succinctness of the target compilation language, and the class of queries and transformations that the language supports in polytime. We then provide a knowledge compilation map, which analyzes a large number of existing target compilation languages according to their succinctness and their polytime transformations and queries. We argue that such analysis is necessary for placing new compilation approaches within the context of existing ones. We also go beyond classical, flat target compilation languages based on CNF and DNF, and consider a richer, nested class based on directed acyclic graphs (such as OBDDs), which we show to include a relatively large number of target compilation languages.

Model-Based Diagnosis using Structured System Descriptions

This paper presents a comprehensive approach for model-based diagnosis which includes proposals for characterizing and computing preferred diagnoses, assuming that the system description is augmented with a system structure (a directed graph explicating the interconnections between system components). Specifically, we first introduce the notion of a consequence, which is a syntactically unconstrained propositional sentence that characterizes all consistency-based diagnoses and show that standard characterizations of diagnoses, such as minimal conflicts, correspond to syntactic variations on a consequence. Second, we propose a new syntactic variation on the consequence known as negation normal form (NNF) and discuss its merits compared to standard variations. Third, we introduce a basic algorithm for computing consequences in NNF given a structured system description. We show that if the system structure does not contain cycles, then there is always a linear-size consequence in NNF which can be computed in linear time. For arbitrary system structures, we show a precise connection between the complexity of computing consequences and the topology of the underlying system structure. Finally, we present an algorithm that enumerates the preferred diagnoses characterized by a consequence. The algorithm is shown to take linear time in the size of the consequence if the preference criterion satisfies some general conditions.

Query DAGs: A Practical Paradigm for Implementing Belief-Network Inference

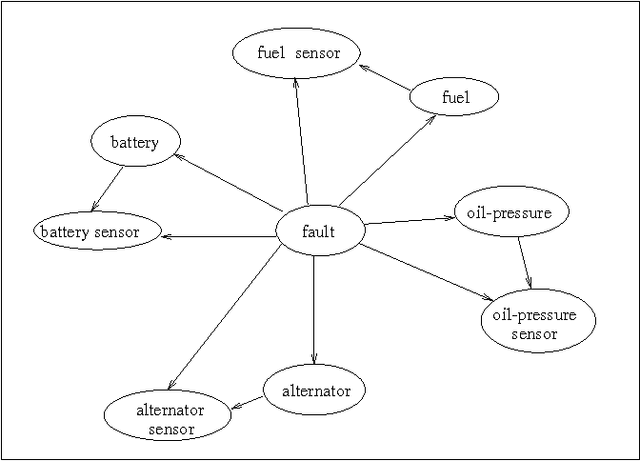
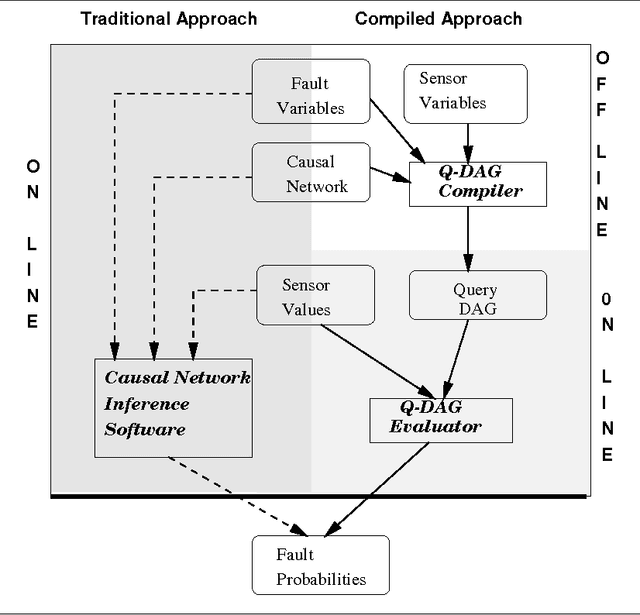
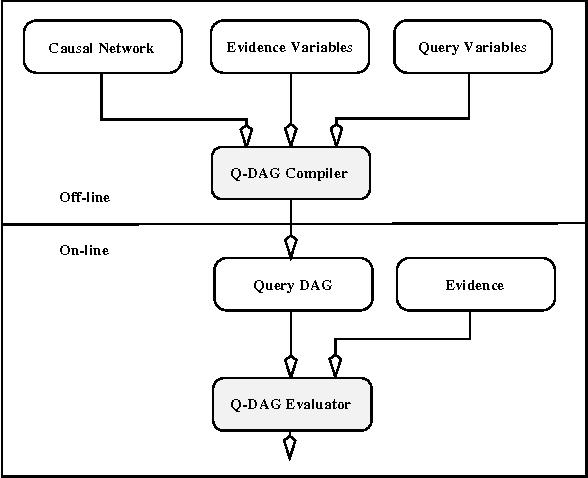
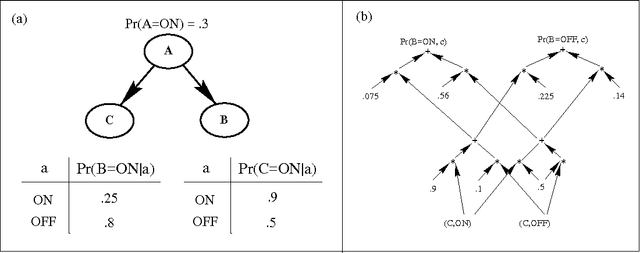
We describe a new paradigm for implementing inference in belief networks, which consists of two steps: (1) compiling a belief network into an arithmetic expression called a Query DAG (Q-DAG); and (2) answering queries using a simple evaluation algorithm. Each node of a Q-DAG represents a numeric operation, a number, or a symbol for evidence. Each leaf node of a Q-DAG represents the answer to a network query, that is, the probability of some event of interest. It appears that Q-DAGs can be generated using any of the standard algorithms for exact inference in belief networks (we show how they can be generated using clustering and conditioning algorithms). The time and space complexity of a Q-DAG generation algorithm is no worse than the time complexity of the inference algorithm on which it is based. The complexity of a Q-DAG evaluation algorithm is linear in the size of the Q-DAG, and such inference amounts to a standard evaluation of the arithmetic expression it represents. The intended value of Q-DAGs is in reducing the software and hardware resources required to utilize belief networks in on-line, real-world applications. The proposed framework also facilitates the development of on-line inference on different software and hardware platforms due to the simplicity of the Q-DAG evaluation algorithm. Interestingly enough, Q-DAGs were found to serve other purposes: simple techniques for reducing Q-DAGs tend to subsume relatively complex optimization techniques for belief-network inference, such as network-pruning and computation-caching.