Zeroth and First Order Stochastic Frank-Wolfe Algorithms for Constrained Optimization

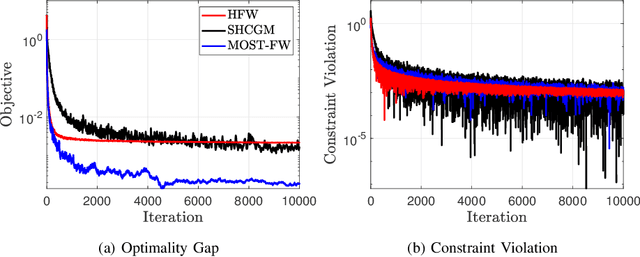
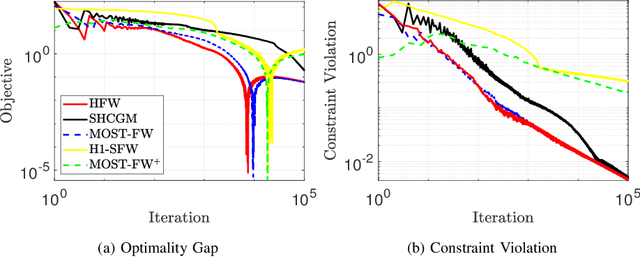
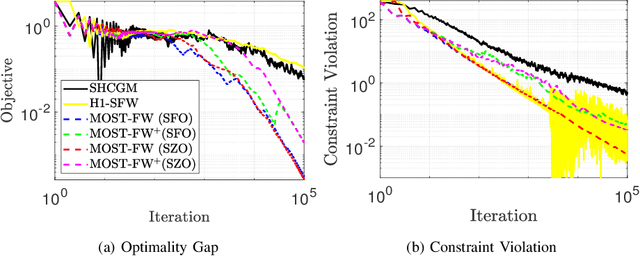
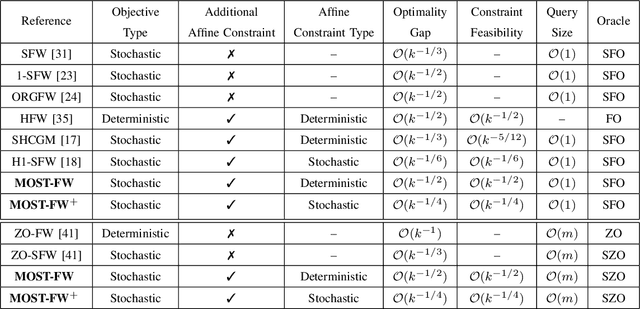
This paper considers stochastic convex optimization problems with two sets of constraints: (a) deterministic constraints on the domain of the optimization variable, which are difficult to project onto; and (b) deterministic or stochastic constraints that admit efficient projection. Problems of this form arise frequently in the context of semidefinite programming as well as when various NP-hard problems are solved approximately via semidefinite relaxation. Since projection onto the first set of constraints is difficult, it becomes necessary to explore projection-free algorithms, such as the stochastic Frank-Wolfe (FW) algorithm. On the other hand, the second set of constraints cannot be handled in the same way, and must be incorporated as an indicator function within the objective function, thereby complicating the application of FW methods. Similar problems have been studied before, and solved using first-order stochastic FW algorithms by applying homotopy and Nesterov's smoothing techniques to the indicator function. This work improves upon these existing results and puts forth momentum-based first-order methods that yield improved convergence rates, at par with the best known rates for problems without the second set of constraints. Zeroth-order variants of the proposed algorithms are also developed and again improve upon the state-of-the-art rate results. The efficacy of the proposed algorithms is tested on relevant applications of sparse matrix estimation, clustering via semidefinite relaxation, and uniform sparsest cut problem.