X-MEN: Guaranteed XOR-Maximum Entropy Constrained Inverse Reinforcement Learning
Paper and Code
Mar 22, 2022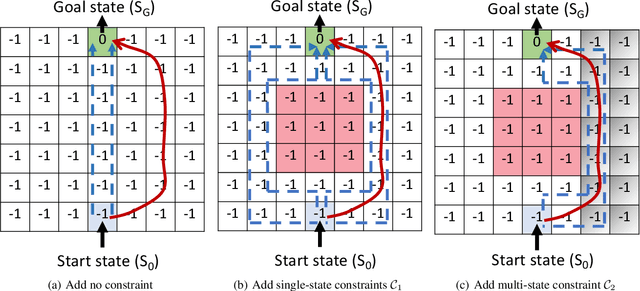
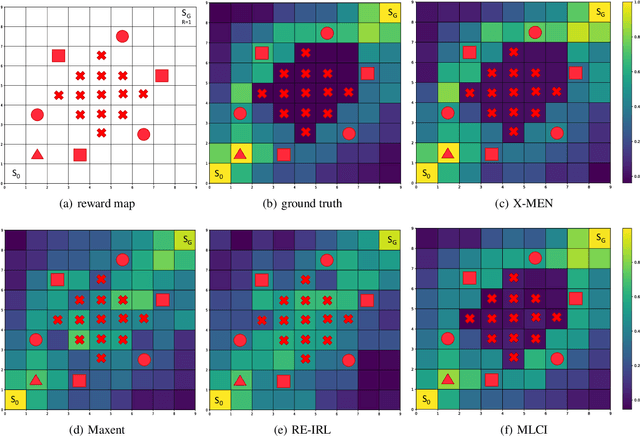
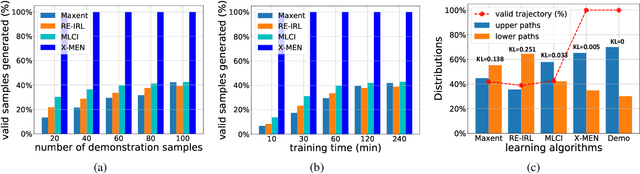
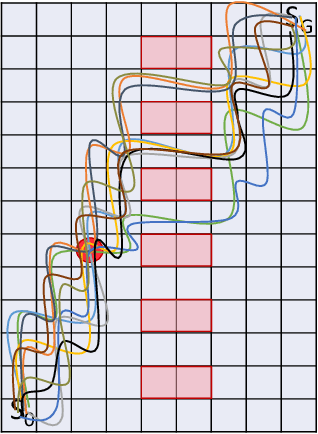
Inverse Reinforcement Learning (IRL) is a powerful way of learning from demonstrations. In this paper, we address IRL problems with the availability of prior knowledge that optimal policies will never violate certain constraints. Conventional approaches ignoring these constraints need many demonstrations to converge. We propose XOR-Maximum Entropy Constrained Inverse Reinforcement Learning (X-MEN), which is guaranteed to converge to the optimal policy in linear rate w.r.t. the number of learning iterations. X-MEN embeds XOR-sampling -- a provable sampling approach that transforms the #P complete sampling problem into queries to NP oracles -- into the framework of maximum entropy IRL. X-MEN also guarantees the learned policy will never generate trajectories that violate constraints. Empirical results in navigation demonstrate that X-MEN converges faster to the optimal policies compared to baseline approaches and always generates trajectories that satisfy multi-state combinatorial constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge