Wind Field Reconstruction with Adaptive Random Fourier Features
Paper and Code
Feb 04, 2021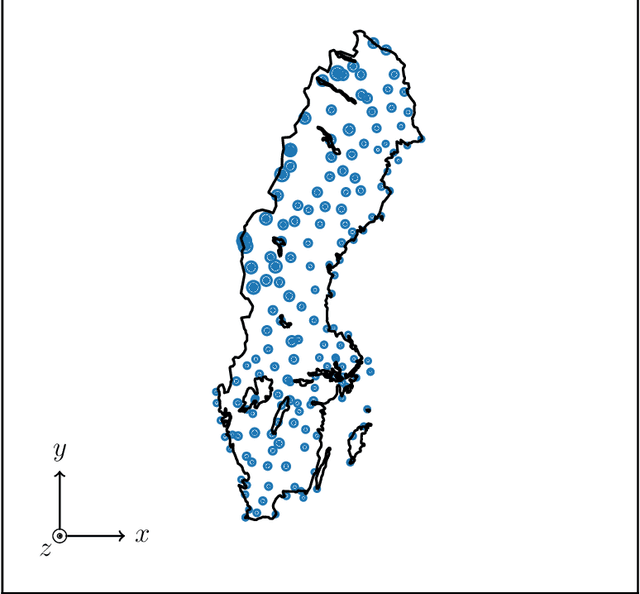
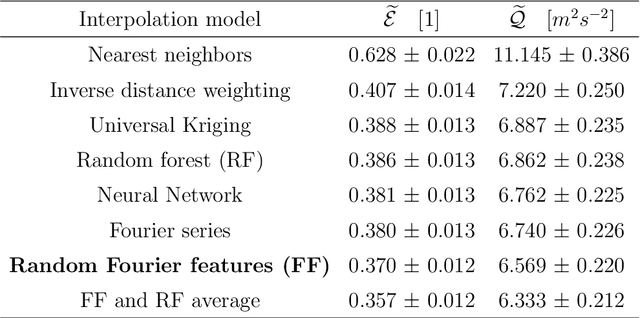
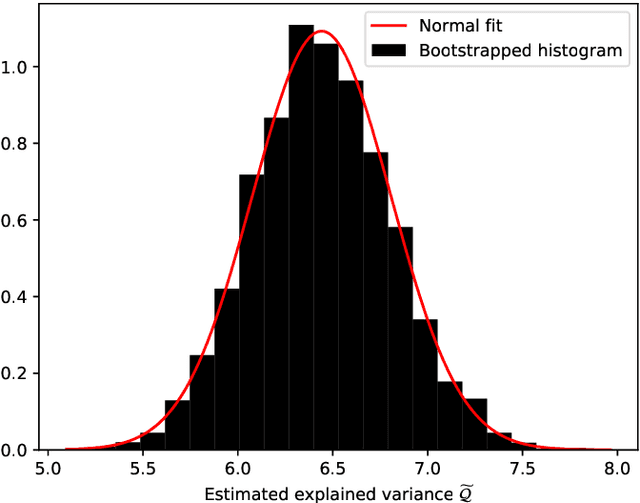
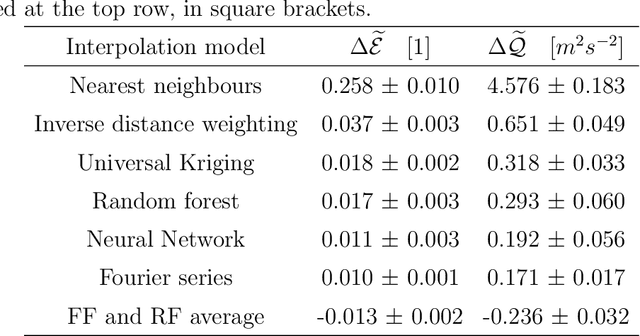
We investigate the use of spatial interpolation methods for reconstructing the horizontal near-surface wind field given a sparse set of measurements. In particular, random Fourier features is compared to a set of benchmark methods including Kriging and Inverse distance weighting. Random Fourier features is a linear model $\beta(\pmb x) = \sum_{k=1}^K \beta_k e^{i\omega_k \pmb x}$ approximating the velocity field, with frequencies $\omega_k$ randomly sampled and amplitudes $\beta_k$ trained to minimize a loss function. We include a physically motivated divergence penalty term $|\nabla \cdot \beta(\pmb x)|^2$, as well as a penalty on the Sobolev norm. We derive a bound on the generalization error and derive a sampling density that minimizes the bound. Following (arXiv:2007.10683 [math.NA]), we devise an adaptive Metropolis-Hastings algorithm for sampling the frequencies of the optimal distribution. In our experiments, our random Fourier features model outperforms the benchmark models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge