Why the Rich Get Richer? On the Balancedness of Random Partition Models

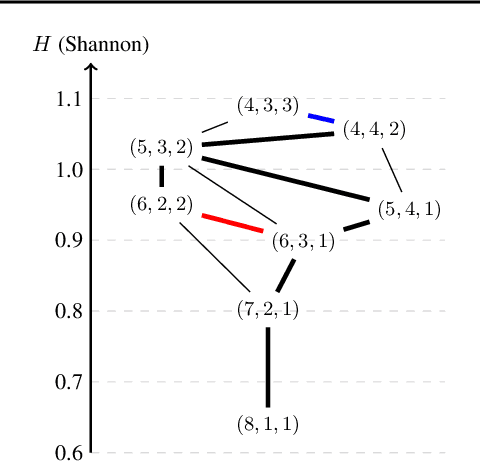
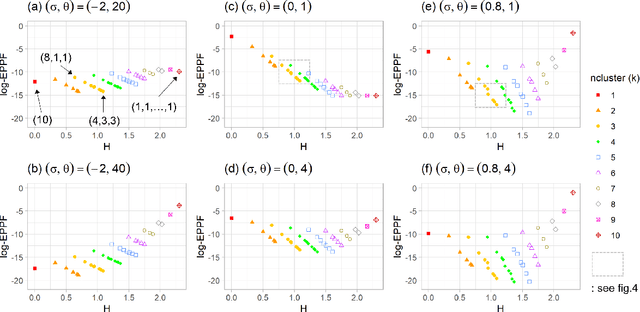
Random partition models are widely used in Bayesian methods for various clustering tasks, such as mixture models, topic models, and community detection problems. While the number of clusters induced by random partition models has been studied extensively, another important model property regarding the balancedness of cluster sizes has been largely neglected. We formulate a framework to define and theoretically study the balancedness of exchangeable random partition models, by analyzing how a model assigns probabilities to partitions with different levels of balancedness. We demonstrate that the "rich-get-richer" characteristic of many existing popular random partition models is an inevitable consequence of two common assumptions: product-form exchangeability and projectivity. We propose a principled way to compare the balancedness of random partition models, which gives a better understanding of what model works better and what doesn't for different applications. We also introduce the "rich-get-poorer" random partition models and illustrate their application to entity resolution tasks.