When Slepian Meets Fiedler: Putting a Focus on the Graph Spectrum
Paper and Code
Mar 21, 2017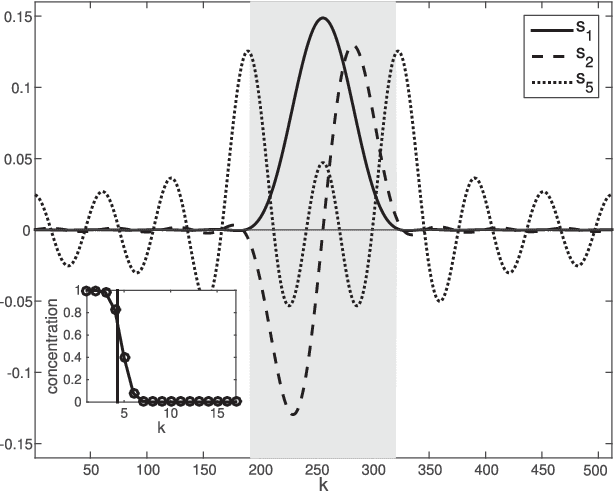


The study of complex systems benefits from graph models and their analysis. In particular, the eigendecomposition of the graph Laplacian lets emerge properties of global organization from local interactions; e.g., the Fiedler vector has the smallest non-zero eigenvalue and plays a key role for graph clustering. Graph signal processing focusses on the analysis of signals that are attributed to the graph nodes. The eigendecomposition of the graph Laplacian allows to define the graph Fourier transform and extend conventional signal-processing operations to graphs. Here, we introduce the design of Slepian graph signals, by maximizing energy concentration in a predefined subgraph for a graph spectral bandlimit. We establish a novel link with classical Laplacian embedding and graph clustering, which provides a meaning to localized graph frequencies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge